Help me!
Cho \(\Delta ABC\) vuông tại A. Gọi D là điểm đối xứng của B qua A, F là trung điểm của AC. Qua D kẻ DE // BC (\(E\in BF\)). Gọi G là trung điểm của DE. BG cắt CD tại H, BE cắt CG tại I, chứng minh \(HI=\frac{1}{4}DE\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 5 2022
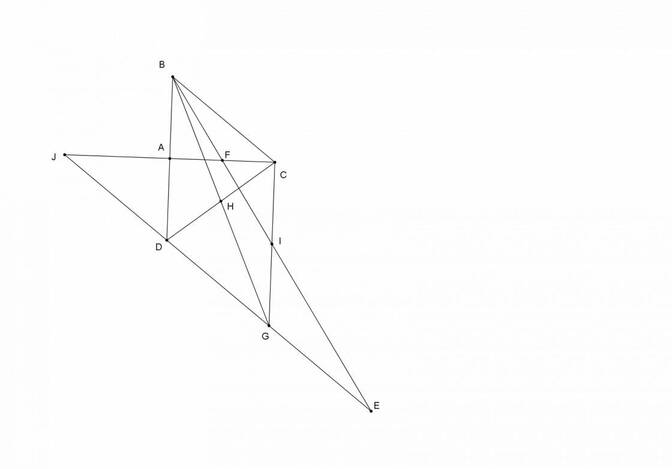
gọi $J$ là giao điểm của $DE,AC$, ta có $BCDJ $là hình thoi nên $BC\parallel JD$, $JA=AC=2CF\Rightarrow 3CF=JF$, theo Thales ta có \(\dfrac{BC}{EJ}=\dfrac{CF}{JF}=\dfrac{1}{3}\Rightarrow JE=3BC\), mà $JD=BC$ nên suy ra $DE=2BC$, hay $EG=DG=BC$, dẫn đến $BCEG,BCGD$ là hình bình hành, suy ra $H$ là trung điểm $CD,I$ là trung điểm $CG$, theo tính chất đường trung bình ta có \(IH=\dfrac{1}{2}DG=\dfrac{1}{4}DE\)
12 tháng 5 2023
a: Xét ΔBAH và ΔBDH có
BA=BD
AH=DH
BH chung
=>ΔBAH=ΔBDH
b: Xét ΔBAE và ΔBDE có
BA=BD
góc ABE=góc DBE
BE chung
=>ΔBAE=ΔBDE
=>DA=DE
9 tháng 12 2023
a: Xét ΔCAB có
E,D lần lượt là trung điểm của CA,CB
=>ED là đường trung bình của ΔCAB
=>ED//AB và \(ED=\dfrac{AB}{2}\)
Ta có: ED//AB
AB\(\perp\)AC
Do đó: ED\(\perp\)AC tại E
=>CA\(\perp\)FD tại E
Xét ΔCFD vuông tại C có CE là đường cao
nên \(FE\cdot FD=CF^2\left(1\right)\)
Xét ΔCFB vuông tại C có CH là đường cao
nên \(FH\cdot FB=FC^2\left(2\right)\)
Từ (1) và (2) suy ra \(FE\cdot FD=FH\cdot FB\)
b: Xét tứ giác AHCB có
\(\widehat{CHB}=\widehat{CAB}=90^0\)
=>AHCB là tứ giác nội tiếp đường tròn đường kính BC
=>\(\widehat{HCA}=\widehat{HBA}\)
=>\(\widehat{ABH}=\widehat{ECH}\)
Xét ΔCHB vuông tại H và ΔFCB vuông tại C có
\(\widehat{CBH}\) chung
Do đó: ΔCHB đồng dạng với ΔFCB
=>\(\dfrac{HB}{CB}=\dfrac{HC}{FC}\)
=>\(\dfrac{HB}{HC}=\dfrac{CB}{FC}\left(1\right)\)
Xét ΔABC vuông tại A và ΔECF vuông tại E có
\(\widehat{ACB}=\widehat{EFC}\left(=90^0-\widehat{CDF}\right)\)
Do đó: ΔABC đồng dạng với ΔECF
=>\(\dfrac{AB}{CE}=\dfrac{BC}{CF}\)(2)
Từ (1) và (2) suy ra \(\dfrac{HB}{HC}=\dfrac{AB}{CE}\)
Xét ΔABH và ΔECH có
\(\dfrac{HB}{HC}=\dfrac{AB}{CE}\)
\(\widehat{HBA}=\widehat{HCE}\)
Do đó: ΔABH đồng dạng với ΔECH
25 tháng 7 2023
Ta có tam giác ABC vuông tại A nên đường cao AH cũng là đường trung tuyến của tam giác ABC. Vậy ta có AH = HD.
Vì D là trung điểm của BC nên BD = CD.
Vì góc DE vuông góc với AC tại E nên tam giác ADE vuông góc tại E.
Vì F là điểm đối xứng của E qua D nên tam giác ADF cũng tại D.
Ta có:
- Tam giác ADE vuông tại E và tam giác ADF vuông tại D có cạnh chung AD.
- Tam giác ADE và tam giác ADF có cạnh AD bằng nhau (vì F là điểm đối xứng của E qua D).
Vậy tam giác ADE và tam giác ADF là hai tam giác cân có cạnh chung AD.
Do đó, ta có AE = AF và DE = DF.
Vì M là trung điểm của HC nên ta có HM = MC.
Vì FM là đường trung tuyến của tam giác HAC nên ta có FM = \(\frac{1}{2}\)AC.
Ta cần chứng minh FM vuông góc với AM.
Ta có:
- Tam giác ADE và tam giác ADF là hai tam giác cân có cạnh chung AD.
- AE = AF và DE = DF.
Do đó, tam giác ADE và tam giác ADF là hai tam giác đồng dạng (theo nguyên tắc đồng dạng cận-cạnh-cạnh).
Do đó, ta có \(\frac{AE}{DE} = \frac{AF}{DF}\).
Vì AE = AF và DE = DF nên ta có \(\frac{AE}{DE} = \frac{AF}{DF} = 1\).
Vậy tam giác ADE và tam giác ADF là hai tam giác đồng dạng cân.
Do đó, ta có góc EAD = góc FAD và góc AED = góc AFD.
Vì góc EAD + góc AED = 90° (do tam giác ADE vuông góc tại E) nên góc FAD + góc AFD = 90°.
Do đó, ta có góc FAM = 90°.
Do đó, FM vuông góc với AM.
29 tháng 9 2016
a/ Dễ thấy ABDC là hình chữ nhật dựa theo dấu hiệu nhận biết.
b/ Dễ thấy.
c/ Ta có EA = AB ; BM = CM => AM là đường trung bình tam giác BCE => AM // CE => AECM là hình thang
d/ Chứng minh được AE = CD ; AE // CD => AECD là hình bình hành
e/ Vì AECD là hình bình hành nên AD // CF => góc CFD = góc FDA (1)
Mặt khác, AM // CE (AMCE là hình thang) mà BF vuông góc với CE => BF vuông góc AM
=> FM là đường cao của tam giác vuông FAD . Từ đó dễ dàng suy ra Góc AFB = góc FDA (2)
Từ (1) và (2) suy ra góc CFD = góc AFB mà góc CFD + góc DFB = 90 độ
=> góc AFB + góc DFB = góc AFD = 90 độ
gfvfvfvfvfvfvfv555