trên con đường đi qua 3 điểm A;B;C......
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Vì cứ qua 2 điểm ta kẻ được 1 và chỉ 1 đường thẳng . Nếu có 2 điểm thẳng hàng , từ 1 điểm kẻ lần lượt với 10 điểm còn lại ta được:
11 . 10 = 110 ( đường thẳng ) . Nhưng như vậy mỗi đường thẳng được tính hai lần nên có số đường thẳng là :
110 : 2 = 55 ( đường thẳng )
b) Vì cứ qua 2 điểm ta kẻ được 1 và chỉ 1 đường thẳng .Nếu có 2 điểm thẳng hàng từ 1 điểm kẻ lần lượt với 10 điểm còn lại ta được:
11 . 10 = 110 ( đường thẳng ) . Nhưng như vậy mỗi đường thẳng được tính hai lần nên có số đường thẳng là :
110 : 2 = 55 ( đường thẳng )
+ Nếu có 5 điểm không thẳng hàng , từ 1 điểm kẻ được với 4 điểm còn lại làm như vậy với 5 điểm ta có : 4 . 5 = 20 ( đường thẳng )
Nhưng vì có điểm thẳng hàng nên 20 đường thẳng này chỉ được tính là 1
Vậy số đường thẳng kẻ được trong đó có 5 điểm thẳng hàng là :
55 - 20 + 1 = 36 ( đường thẳng )

A D M E C N B P
a) Ta có: ID vuông góc AM với D là trung điểm AM => ID là đường trung trực AM => IA = IM (1)
IE vuông góc AN với E là trung điểm AN => IE là đường trung trực AN => IA = IN (2)
Từ (1) và (2) => IA = IM = IN
=> I là tâm đường tròn qua 3 điểm A; M; N
b. Lấy điểm P đối xứng với điểm A qua BC => P cố định
=> BC là đường trung trực của PA mà I thuộc BC
=> IP = IA
=>( I) qua điểm P cố định khác A

Để vẽ được các đường thẳng như yêu cầu, chúng ta có thể sử dụng nguyên tắc "mỗi đường thẳng đi qua 2 trong 4 điểm trên".
a. Để vẽ 6 đường thẳng, ta có thể chọn 2 điểm từ 4 điểm trên và vẽ đường thẳng đi qua chúng. Vì có 4 điểm, ta có C(4,2) = 6 cách chọn 2 điểm từ 4 điểm trên. Vậy, ta có thể vẽ được 6 đường thẳng.
b. Tương tự, để vẽ 4 đường thẳng, ta có C(4,2) = 6 cách chọn 2 điểm từ 4 điểm trên. Vậy, ta có thể vẽ được 4 đường thẳng.
c. Để vẽ 2 đường thẳng, ta cũng có C(4,2) = 6 cách chọn 2 điểm từ 4 điểm trên. Vậy, ta có thể vẽ được 2 đường thẳng.
Với các yêu cầu trên, chúng ta có thể vẽ được số đường thẳng tương ứng.

a, 6 đường thẳng
b, 28 đường thẳng
c, \(\frac{n.\left(n-1\right)}{2}\)đường thẳng

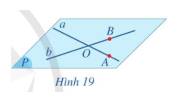
a) Mặt phẳng đi qua ba điểm A. B, O đi qua hai đường thẳng a và b
b) Có một và chỉ một mặt phẳng đi qua hai đường thẳng a và b


Huy làm có gì sai mọi người góp ý nha :3
a
Ta có 2 đường trung trực của các đoạn thẳng AM,AN cắt nhau tại I nên I là tâm đường tròn ngoại tiếp tam giác AMN
b
Hạ đường cao AK. Gọi L đối xứng với A qua K. Suy ra L cố định.Ta sẽ chứng minh tứ giác AMLN nội tiếp. Thật vậy !
Ta dễ có được đường tròn tâm I ngoại tiếp tam giác ALN
Ta có:\(\widehat{AIN}=2\widehat{ALN};\widehat{AIN}=2\widehat{AMN}\Rightarrow\widehat{ALN}=\widehat{AMN}\) nên tứ giác AMLN nội tiếp khi đó đường tròn I luôn đi qua điểm L cố định
Hình tui đã vẽ trong TKHĐ nhé :))
Mình làm ra vở cho bạn rồi nhé. Chữ mình hơi xấu, mong bạn thông cảm.
thế nào nữa bạn ơi
vì mình muốn giúp bạn
LƯU Ý
Các bạn học sinh KHÔNG ĐƯỢC đăng các câu hỏi không liên quan đến Toán, hoặc các bài toán linh tinh gây nhiễu diễn đàn. Online Math có thể áp dụng các biện pháp như trừ điểm, thậm chí khóa vĩnh viễn tài khoản của bạn nếu vi phạm nội quy nhiều lần.
Chuyên mục Giúp tôi giải toán dành cho những bạn gặp bài toán khó hoặc có bài toán hay muốn chia sẻ. Bởi vậy các bạn học sinh chú ý không nên gửi bài linh tinh, không được có các hành vi nhằm gian lận điểm hỏi đáp như tạo câu hỏi và tự trả lời rồi chọn đúng.
Mỗi thành viên được gửi tối đa 5 câu hỏi trong 1 ngày
Các câu hỏi không liên quan đến toán lớp 1 - 9 các bạn có thể gửi lên trang web h.vn để được giải đáp tốt hơn.