gọi A là tập hợp gồm 100 số nguyên dương đầu tiên. hãy chọn từ tập A 10 số sao cho không có 3 số nào trong các số được chọn là độ dài 3 cạnh của tam giác
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 8 2017
Phương pháp:
Công thức tính xác suất của biên cố A là: P A = n A n Ω
Gọi A là biến cố: “Chọn ngẫu nhiên 3 phần tử của tập S sao cho tổng của 3 phần tử chia hết cho 3”.
Trong tập hợp S có 5 số chia hết cho 3 là
TH4: Trong 3 số a, b, c có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2
CM
26 tháng 11 2018
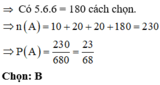
Đáp án B.
*Đa giác lồi (H) có 22 cạnh nên cũng có 22 đỉnh. Số tam giác có 3 đỉnh là đỉnh của đa giác (H) là C 22 3 = 1540 (tam giác)
Suy ra số phàn tử của không gian mẫu Ω là n ( Ω ) = C 1540 2 .
*Số tam giác của một cạnh là cạnh của đa giác (H) là 22.18 = 396 (tam giác).
Số tam giác có hai cạnh là cạnh của đa giác (H) là 22 (tam giác)
Số tam giác không có cạnh nào là cạnh của đa giác (H) là:
1540 – 396 – 22 = 1122 (tam giác).
Gọi A là biến cố “Hai tam giác được chọn có 1 cạnh là cạnh của đa giác (H) và 1 tam giác không có cạnh nào là cạnh của đa giác (H)”
Số phần tử của A là n ( A ) = C 396 1 . C 1122 1 .
*Vậy xác suất cần tìm là
P ( A ) = n ( A ) n ( Ω ) = C 396 1 . C 1122 1 C 1540 2 = 748 1995 ≈ 0,375.
CM
28 tháng 1 2017
Đáp án B
Khi đó
- Số cách chọn chữ số α có 5 cách chọn vì α ≠ 0 .
- Số cách chọn chữ số b có 5 cách chọn vì b ≠ α .
- Số cách chọn chữ số c có cách chọn vì c ≠ α và c ≠ b .
Do đó tập S có 5.5.4 = 100 phần tử.
Không gian mẫu là chọn ngẫu nhiên1 số từ tập S .
Suy ra số phần tử của không gian mẫu là Ω = C 100 1 = 100 .
Gọi X là biến cố "Số được chọn có chữ số cuối gấp đôi chữ số đầu". Khi đó ta có các bộ số là 1 b 2 hoặc 2 b 4 thỏa mãn biến cố X và cứ mỗi bộ thì b có 4 cách chọn nên có tất cả số thỏa yêu cầu.
Suy ra số phần tử của biến cố X là Ω X = 8 .
Vậy xác suất cần tính P ( X ) = Ω X Ω = 8 100 = 2 25 .
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
a) Số nguyên dương nhỏ hơn 100 luôn có 1 hoặc 2 chữ số nên ta có không gian mẫu của phép thử trên là: \(\Omega = \left\{ {1,2,3,4,5,...98,99} \right\}\)
b) Tập hợp biến cố A: “Số được chọn là số chính phương” là:
\(A = \left\{ {{a^2}\left| {a = 1,2,...,9} \right.} \right\}\)
c) Cứ 4 số thì có 1 số chia hết cho 4, số nhỏ nhất là 4 và lớn nhất là 96 nên số kết quả thuận lợi cho biến cố B là \(\dfrac{96-4}{4}+1=24\).
Vậy có 24 kết quả thuận lợi cho biến cố B: “Số được chọn chia hết cho 4”
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
27 tháng 9 2023
\(a,\Omega=\left\{1;2;3;4;5;...;98;99\right\}\\ b,A=\left\{1;4;9;16;25;36;49;64;81\right\}\\c, B=\left\{4;8;16;20;24;...;92;96\right\}\\ Số.kết.quả.thuận.lợi.cho.B:\left(96-4\right):4+1=24\left(kết.quả\right)\)