Cho tam giác ABC có 2 đường cao CP và BQ cắt nhau tại H.Gọi M là trung điểm của BC. a) CM tứ giác BPQC nội tiếp. b) Gọi D là điểm đối xứng với C qua H.Đường thẳng đi qua H vuông góc với HM cắt AB,AC theo thứ tự tại E,F. CM rằng : DE vuông góc BH. c) CM ME = MF.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 3 2023
Kẻ CG//MN(G thuộc AB), CG cắt AD tại K
=>HI vuông góc CK
=>I là trựctâm của ΔHCK
=>KI vuông góc CH
=>KI//AB
=>KI//BG
=>K là trung điểm của CG
MN//GC
=>MH/GK=HN/KC
mà GK=KC
nên MH=HN
CM
10 tháng 8 2017
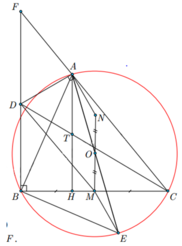
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .
a: Xét tứ giác BPQC có
\(\widehat{BPC}=\widehat{BQC}=90^0\)
Do đó: BPQC là tứ giác nội tiếp
Giải chi tiết đc ko ạ