Tìm số nguyên x và y sao cho: (x+2)(y-1)=7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a.x=1;y=9\)
\(b. (x-6). (y+2)=7\)
Ta lập bảng :
| \(x-6\) | \(1\) | \(-1\) | \(7\) | \(-7\) |
| \(y+2\) | \(7\) | \(-7\) | \(1\) | \(-1\) |
| \(x \) | \(7\) | \(5\) | \(13\) | \(-1\) |
| \(y\) | \(5\) | \(-9\) | \(-1\) | \(-3\) |
\(Vậy :..........\)
a) Vì x, y nguyên mà x.y = 9 nên x, y thuộc Ư(9)
Mà x< y. Ta có bảng sau
| x | 1 | -9 |
| y | 9 | -1 |
Vậy (x,y) \(\in\){(1;9) , ( -9; -1) }
b) vì x, y nguyên suy ra x-6 , y + 2 nguyên
mà (x-6). ( y+2) =7
nên (x-6), ( y+2) thuộc Ư(7) .Ta lập bảng như sau
| x-6 | 1 | -1 | 7 | -7 |
| y+2 | 7 | -7 | 1 | -1 |
| x | 7 | 5 | 13 | -1 |
| y | 5 | -9 | -1 | -3 |
Tự kết luận nhé

a )
(x-3).(2y+1)=7
(x-3).(2y+1)= 1.7 = (-1).(-7)
Cứ cho x - 3 = 1 => x= 4
2y + 1 = 7 => y = 3
Tiếp x - 3 = 7 => x = 10
2y + 1 = 1 => y = 0
x-3 = -1 ...
1.tìm các số nguyên x và y sao cho:
(x-3).(2y+1)=7
Vì x;y là số nguyên =>x-3 ; 2y+1 là số nguyên
=>x-3 ; 2y+1 C Ư(7)
ta có bảng:
| x-3 | 1 | 7 | -1 | -7 |
| 2y+1 | 7 | 1 | -7 | -1 |
| x | 4 | 10 | 2 | -4 |
| y | 3 | 0 | -4 | -1 |
Vậy..............................................................................
2.tìm các số nguyên x và y sao cho:
xy+3x-2y=11
x.(y+3)-2y=11
x.(y+3)-y=11
x.(y+3)-(y+3)=11
(x-1)(y+3)=11
Vì x;y là số nguyên => x-1;y+3 là số nguyên
=> x-1;y+3 Thuộc Ư(11)
Ta có bảng:
| x-1 | 1 | 11 | -1 | -11 |
| y+3 | 11 | 1 | -11 | -1 |
| x | 2 | 12 | 0 | -10 |
| y | 8 | -2 | -14 | -4 |
Vậy.......................................................................................

2)
Tổng của 2 số là 2009
=> Trong 2 số phải có 1 số chẵn và 1 số lẻ
Mà số nguyên tố chẵn duy nhất là 2
=> 1 số là 2. Số còn lại là:
2009 - 2 = 2007 không là số nguyên tố
=> Tổng của 2 số nguyên tố không thể bằng 2009.
1)
Với p = 2 => p + 2 = 2 + 2 = 4 là hợp số (loại)
Với p = 3 => p + 2 = 3 + 2 = 5 là SNT
=> p + 4 = 3 + 4 = 7 là SNT (thỏa mãn)
Với p > 3 => p có dạng 3k + 1 hoặc 3k + 2 (k ∈ N*)
Nếu p = 3k + 1 => p + 2 = 3k + 1 + 2 = 3k + 3 chia hết cho 3 và lớn hơn 3
=> p + 2 là hợp số (loại)
Nếu p = 3k + 2 => p + 4 = 3k + 2 + 4 = 3k + 6 chia hết cho 3 và lớn hơn 3
=> p + 4 là hợp số (loại)
Vậy p = 3


a: \(\left(x,y\right)\in\left\{\left(1;2\right);\left(-1;-2\right);\left(2;1\right);\left(-2;-1\right)\right\}\)
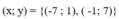
=>y∈{2;8;0;-6}
=>x∈{5;-1;-9;-3}
- Xin lỗi mình đang bận nên không giải chi tiết được :)