Cho hai phân số \(\frac{6}{x}\) và \(\frac{24}{x-27}\). Với giá trị nguyên nào của x thì hai phân số trên bằng nhau?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có \(\frac{6}{x}=\frac{24}{x-27}\Leftrightarrow\frac{24}{4x}=\frac{24}{x-27}\Rightarrow4x=x-27\)
\(\Rightarrow27=x-4x\Rightarrow x=-9\)

Ta có:
\(\frac{6}{x}=\frac{24}{x-27}\)
\(\Rightarrow6.\left(x-27\right)=24.x\)
\(\Rightarrow6x-162=24x\)
\(\Rightarrow6x-24x=162\)
\(\Rightarrow-18x=162\)
\(\Rightarrow x=-9\)
Vậy x = -9 thì 2 phân số trên bằng nhau

Nếu:\(\frac{2}{x}=\frac{2}{x+2}\)
=>\(2x+4=2x\)
\(0x=-4\)(vô lí)
Vậy không có giá trị n để thỏa mãn đề bài

a) Chia cả tử và mẫu của phân số \(\frac{{ - 20}}{{30}}\) cho -5 thì được phân số \(\frac{4}{{ - 6}}\)
b) Hai phân số này bằng nhau, vì \[ - 20.( - 6) = {\rm{ }}4.30\]
c) Ví dụ: Phân số \(\frac{{ - 9}}{{12}}\) và phân số \(\frac{{ - 3}}{4}\)

a) Nhân cả tử và mẫu của phân số \(\frac{3}{{ - 5}}\) với số -7 thì được phân số \(\frac{{ - 21}}{{35}}\).
b) Hai phân số trên bằng nhau, vì \[3.35{\rm{ }} = {\rm{ }} - 5.( - 21)\]
c) Ví dụ: Phân số \(\frac{{ - 2}}{5}\) và phân số \(\frac{4}{{ - 10}}\) (Nhân cả tử và mẫu của phân số \(\frac{{ - 2}}{5}\) với -2 được phân số \(\frac{4}{{ - 10}}\)

+ Giá trị của phân thức x - 2 x 2 - 5 x + 6 được xác định khi và chỉ khi x 2 - 5 x + 6 ≠ 0
⇔ ( x - 3 )( x - 2 ) ≠ 0 hay x ≠ 2,x ≠ 3.
+ Giá trị của phân thức 1/(x - 3) được xác định khi và chỉ khi x - 3 ≠ 0 hay x ≠ 3.
Với x ≠ 2,x ≠ 3 ta có: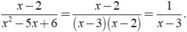
Vậy với x ≠ 2,x ≠ 3 ta có: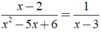
Chọn đáp án C.