cho 2 dây AB và CD của đường tròn O cắt nhau tại M . chứng minh MA.MB=MC.MD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
OW
26 tháng 1 2016
Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath
CM
11 tháng 1 2018
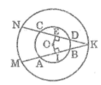
Kẻ OI ⊥ AB, OE ⊥ CD
Trong (O; OA) ta có: AB < CD (gt)
Suy ra : OI > OE (dây lớn hơn gần tâm hơn)
Trong (O ; OK) ta có : OI > OE (cmt)
Suy ra : KM < KN (dây gần tâm hơn thì lớn hơn)
CM
10 tháng 6 2019
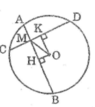
Ta có: HA = HB (gt)
Suy ra : OH ⊥ AB (đường kính dây cung)
Lại có : KC = KD (gt)
Suy ra : OK ⊥ CD (đường kính dây cung)
Mà AB > CD (gt)
Nên OK > OH (dây lớn hơn gần tâm hơn)
Áp dụng định lí Pitago vào tam giác vuông OHM ta có :
O M 2 = O H 2 + H M 2
Suy ra : H M 2 = O M 2 - O H 2 (1)
Áp dụng định lí Pitago vào tam giác vuông OKM ta có:
O M 2 = O K 2 + K M 2
Suy ra: K M 2 = O M 2 - O K 2 (2)
Mà OH < OK (cmt) (3)
Từ (1), (2) và (3) suy ra: H M 2 > K M 2 hay HM > KM
Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn \(\stackrel\frown{BC}\)
\(\widehat{BDC}\) là góc nội tiếp chắn \(\stackrel\frown{BC}\)
Do đó: \(\widehat{BAC}=\widehat{BDC}\)(Hệ quả)
hay \(\widehat{MAC}=\widehat{MDB}\)
Xét ΔMAC và ΔMDB có
\(\widehat{MAC}=\widehat{MDB}\)(cmt)
\(\widehat{AMC}\) chung
Do đó: ΔMAC∼ΔMDB(g-g)
Suy ra: \(\dfrac{MA}{MD}=\dfrac{MC}{MB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(MA\cdot MB=MC\cdot MD\)(đpcm)