Với giá trị nào của x thì ta có x2 < x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 11 2021
\(M=x^2+2x-8-x^3+x^3=x^2+2x-8=\left(x^2+2x+1\right)-9=\left(x+1\right)^2-9\ge-9\)
\(minM=-9\Leftrightarrow x=-1\)
5 tháng 11 2021
\(M=x^2+2x-8-x^3+x^3=\left(x^2+2x+1\right)-9=\left(x+1\right)^2-9\ge-9\\ M_{min}=-9\Leftrightarrow x=-1\)
CM
12 tháng 8 2018
Ta có: x 2 - 2 3 x - 3 = 2 x 2 +2x + 3
⇔ x 2 - 2 3 x - 3 - 2 x 2 -2x - 3 =0
⇔ x 2 +2x +2 3 x +2 3 =0
⇔ x 2 + 2(1 + 3 )x + 2 3 =0
∆ ' = b ' 2 – ac= 1 + 3 2 – 1. 2 3 = 1 + 2 3 + 3 -2 3 = 4 > 0
∆ ' = 4 =2
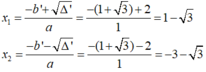
Vậy với x=1 - 3 hoặc x = - 3 - 3 thì giá trị của hai biểu thức trên bằng nhau
CM
6 tháng 5 2017
a) x ≠ -5.
b) Ta có P = ( x + 5 ) 2 x + 5 = x + 5
c) Ta có P = 1 Û x = -4 (TMĐK)
d) Ta có P = 0 Û x = -5 (loại). Do vậy x ∈ ∅ .
LM
4
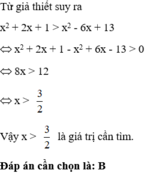
Ko có giá trị vì
X x X > X hoặc X x X = X thôi
Ta luôn có: \(x^2\ge x\) với
Vx, không có nhỏ hơn.