Câu 13. Một cây dừa nặng 480 N được bắc qua một con mương. Trong t in cây dừa cách liểm tựa A là 2 m và cách điểm tựa B là 1 m. Hỏi lực mà cây dừa tác dụ n điểm tựa A và điểm tựa B bằng bao nhiêu? A. F_{1} = 180Nvi F_{2} = 300N B. F_{1} = 320N * v_{2} F_{2} = 160N C. F_{1} = 300N và F_{2} = 180N D. F_{1} = 160N và F_{2} = 320 N.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 12 2015
Áp dụng công thức: \(\frac{F_A}{F_B}=\frac{d_B}{d_A}=\frac{1,2}{2,4}=\frac{1}{2}\)(1)
Mà \(F_A+F_B=P=240N\)(2)
Từ (1) và (2) suy ra: \(F_A=80N\)
VT
9 tháng 9 2019
Chọn B.
Biểu diễn lực như hình vẽ sau:
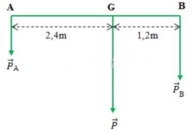
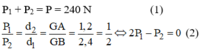
Giải hệ (1) và (2) ta được: P1 = 80 N; P2 = 160 N
VT
10 tháng 4 2019
Đáp án C
Gọi F 1 , F 2 là độ lớn của hai lực đặt lên hai đầu điểm tựa A và B.
F 1 , F 2 lần lượt cách vai là d 1 = 60 cm, d 2 = 40 cm.
Ta có: F 1 + F 2 = 1000 (1)
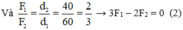
Từ (1) và (2) → F 1 = 400 N, F 2 = 600 N
16 tháng 4 2017
Tương tự bài 3. P = PA + PB = 240 (1)
PA. GA = PB.GB
=> PB = PA. = 2 PA (2)
(1) và (2) => P = 3 PA => PA == 80N
Chọn B
AM
27 tháng 12 2021
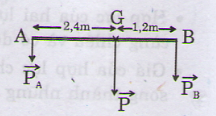
Ta có: \(F_A.OA=F_B.OB\)
\(\Leftrightarrow OA.\left(P-F_B\right)=OB.F_B\)
\(\Leftrightarrow0,4.\left(200-F_B\right)=0,6.F_B\)
\(\Rightarrow F_B=80N\)
23 tháng 2 2022
Theo bài: \(AG=2,4m\)
\(BG=4,4-2,4=2m\)
Áp dụng quy tắc momen lực:
\(P_A\cdot AG=P_B\cdot BG\) \(\Rightarrow2,4P_A=2P_B\left(1\right)\)
Mà \(P_A+P_B=2200\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}P_A=1000N\\P_B=1200N\end{matrix}\right.\)
Chọn A
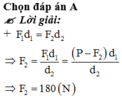
Ai help voi em đang kiểm tra :((