Cho tam giac ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE a) Chứng minh tam giác ADE là tam giác cân b)Kẻ BH vuông góc với AD Kẻ CK vuông góc AE Chứng minh rằng BH=CK,AH=AK c)Gọi I là giao điểm của BH và CK.TAm giác IBC là tam giác gì? Vì saoe) Khi góc BAC =60độ và BD=CE=BC hãy tính số đo các góc của tam giác ADE và xác định dạng tam giác IBC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 8 2023
a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
=>ΔADE cân tại A
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB=góc KAC
=>ΔAHB=ΔAKC
=>AH=AK
Xét ΔADE có AH/AD=AK/AE
nên HK//DE
c:
góc HBD+góc D=90 độ
góc KCE+góc E=90 độ
mà góc D=góc E
nên góc HBD=góc KCE
góc MBC=góc HBD
góc MCB=góc KCE
mà góc HBD=góc KCE
nên góc MBC=góc MCB
=>ΔMBC cân tại M
4 tháng 2 2022
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó; ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔABH=ΔACK
Suy ra: BH=CK
b: Ta có: ΔABH=ΔACK
nên \(\widehat{ABH}=\widehat{ACK}\)
c: Ta có: \(\widehat{OBC}=\widehat{HBD}\)
\(\widehat{OCB}=\widehat{KCE}\)
mà \(\widehat{HBD}=\widehat{KCE}\)
nên \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
20 tháng 2 2021
a) Ta có: \(\widehat{ABC}+\widehat{ABD}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACE}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(Hai góc ở đáy của ΔBAC cân tại A)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
AB=AC(ΔABC cân tại A)
\(\widehat{ABD}=\widehat{ACE}\)(cmt)
BD=CE(gt)
Do đó: ΔABD=ΔACE(c-g-c)
Suy ra: AD=AE(hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
b) Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE(gt)
\(\widehat{HDB}=\widehat{KEC}\)(ΔADB=ΔAEC)
Do đó: ΔHBD=ΔKCE(cạnh huyền-góc nhọn)
c) Ta có: ΔHBD=ΔKCE(cmt)
nên \(\widehat{HBD}=\widehat{KCE}\)(hai góc tương ứng)
mà \(\widehat{HBD}=\widehat{OBC}\)(hai góc đối đỉnh)
và \(\widehat{KCE}=\widehat{OCB}\)(hai góc đối đỉnh)
nên \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định nghĩa tam giác cân)
21 tháng 1 2023
a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔADB=ΔAEC
=>AD=AE
=>ΔADE cân tại A
b,c: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB=góc KAC
=>ΔAHB=ΔAKC
=>BH=CK
Xét ΔAMB vuông tại M và ΔANC vuông tại N có
AB=AC
góc MAB=góc NAC(góc MAB=góc MAC+góc BAC;góc NAC=góc NAB+góc BAC;gócMAC=góc NAB)
=>ΔAMB=ΔANC
=>BM=CN
d: Xét ΔADE có AH/AD=AK/AE
nên HK//DE
=>HK//BC
21 tháng 1 2023
a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
góc D=góc E
=>ΔBHD=ΔCKE
=>BH=CK
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
BH=CK
=>ΔAHB=ΔAKC
31 tháng 1 2022
a) Xét \(\Delta ADB\) và \(\Delta AEC\) có:
\(AB=AC\) (do \(\Delta ABC\) cân tại \(A\))
\(\widehat{ABD}=\widehat{ACE}\)
\(BD=CE\) (giả thiết)
\(\Rightarrow\Delta ADB=\Delta AEC\left(c.g.c\right)\)
\(\Rightarrow AD=AE\) (\(2\) cạnh tương ứng)
\(\Rightarrow\Delta ADE\) cân tại \(A\)
b) Vì \(\Delta ADE\) cân tại \(A\)
\(\Rightarrow\widehat{ADB}=\widehat{ACE}\) (\(2\) góc tương ứng)
Ta có: \(\left\{{}\begin{matrix}\widehat{ADB}+\widehat{HBD}=90^o\\\widehat{ACE}+\widehat{KCE}=90^o\end{matrix}\right.\) (\(2\) góc phụ nhau)
Từ hai điều trên \(\Rightarrow\widehat{HBD}=\widehat{KCE}\)
Mà \(\left\{{}\begin{matrix}\widehat{HBD}=\widehat{CBI}\\\widehat{KCE}=\widehat{BCI}\end{matrix}\right.\) (\(2\) góc đối đỉnh)
Từ đó \(\Rightarrow\widehat{CBI}=\widehat{BCI}\)
\(\Rightarrow\Delta BIC\) cân tại \(I\)
c) Xét \(\Delta ABI\) và \(\Delta ACI\) có:
\(AB=AC\) (giả thiết)
\(BI=CI\) (do \(\Delta BIC\) cân tại \(I\))
\(AI\) là cạnh chung
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\Rightarrow\widehat{AIB}=\widehat{AIC}\) (\(2\) góc tương ứng)
\(\Rightarrow AI\) là tia phân giác \(\widehat{BIC}\)
CM
17 tháng 5 2018
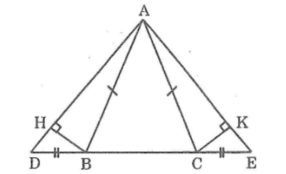
Vì ΔABC cân tại A nên∠(ABC) =∠(ACB) (tính chất tam giác cân)
Ta có: ∠(ABC) +∠(ABD) =180o(hai góc kề bù)
∠(ACB) +∠(ACE) =180o(hai góc kề bù)
Suy ra: ∠(ABD) =∠(ACE)
Xét ΔABD và ΔACE, ta có:
AB = AC (gt)
∠(ABD) =∠(ACE) (chứng minh trên)
BD=CE (gt)
Suy ra: ΔABD= ΔACE (c.g.c)
⇒∠D =∠E (hai góc tương ứng)
Xét hai tam giác vuông ΔBHD và ΔCKE, ta có:
∠(BHD) =∠(CKE) = 90º
BD=CE (gt)
∠D =∠E (chứng minh trên)
Suy ra: ΔBHD= ΔCKE (cạnh huyền – góc nhọn)
Suy ra: BH = CK (hai cạnh tương ứng)
10 tháng 1 2022
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Dođó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔAHB=ΔAKC
Suy ra: BH=CK và AH=AK
Xét ΔADE có
AH/AD=AK/AE
Do đó: HK//DE
hay HK//BC
c: Ta có: \(\widehat{OBC}=\widehat{HBD}\)
\(\widehat{OCB}=\widehat{KCE}\)
mà \(\widehat{HBD}=\widehat{KCE}\)
nên \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
Bạn tự vẽ hình nha!
a.
Ta có:
mà B1 = C1 (tam giác ABC cân tại A)
=> B2 = C2 (1)
Xét tam giác ADB và tam giác AEC:
AB = AC (tam giác ABC cân tại A)
B2 = C2 (theo 1)
BD = CE (gt)
=> Tam giác ADB = ACE (c.g.c)
=> AD = AE (2 cạnh tương ứng)
=> Tam giác ADE
b.
Xét tam giác AHB vuông tại A và tam giác AKC vuông tại K:
AB = AC (tam giác ABC cân tại A)
A1 = A2 (tam giác ADB = tam giác AEC)
=> Tam giác AHB = Tam giác AKC (cạnh huyền - góc nhọn)
=> BH = CK (2 cạnh tương ứng)
AH = AK (2 cạnh tương ứng)
c.
Xét tam giác HDB vuông tại H và tam giác KEC vuông tại K:
BH = CK (theo câu b)
BD = CE (gt)
=> Tam giác HDB = Tam giác KEC (cạnh huyền - cạnh góc vuông)
Ta có:
DBH = IBC (2 góc đối đỉnh)
KCE = ICB (2 góc đối đỉnh)
mà DBH = KCE (tam giác HDB = tam giác KEC)
=> IBC = ICB
=> Tam giác IBC cân tại I