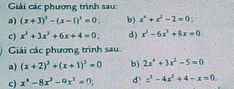
mn giúp em với ah
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đề bài mờ quá em ơi, em chụp màn hình máy tính rồi up lại hoặc đánh rõ tên đề bài ra để mn cùng giúp nhé!
Em đăng lại bài rồi đấy ah chị giúp em với ah đề bài là cô chụp trên máy rồi cô gửi em chứ k phải em tự chụp ạ






Lời giải:
Bổ sung điều kiện $x$ nguyên.
Ta có:
$2x+7\vdots x-2$
$\Rightarrow 2(x-2)+11\vdots x-2$
$\Rightarrow 11\vdots x-2$
$\Rightarrow x-2\in \left\{1; -1; 11; -11\right\}$
$\Rightarrow x\in \left\{3; 1; 13; -9\right\}$

a) Ta có: \(\widehat{BAC}+\widehat{xAC}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{xAC}=100^0\)
\(\Leftrightarrow\widehat{xAt}=\widehat{CAt}=\dfrac{\widehat{xAC}}{2}=\dfrac{100^0}{2}=50^0\)
b) Ta có: \(\widehat{CAt}=\widehat{BCA}\left(=50^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên At//BC(Dấu hiệu nhận biết hai đường thẳng song song)

A B C x y
Vì BC và Cx là 2 tia đối nên \(\widehat{BCA}\) và \(\widehat{ACx}\) là 2 góc kề bù
\(\Rightarrow\widehat{ACB}+\widehat{ACx}=180^o\)
\(40^o+\widehat{ACx}=180^o\)
\(\widehat{ACx}=140^o\)
b) Ta có:\(\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\) (tổng 3 góc trong 1 tam giác)
\(40^o+\widehat{ABC}+70^o=180^o\)
\(\widehat{ABC}=70^o\)(1)
Vì Oy là phân giác của \(\widehat{ACx}\) nên \(\widehat{xCy}=\dfrac{\widehat{ACx}}{2}=\dfrac{140^o}{2}=70^o\)(2)
Từ (1),(2) => \(\widehat{ABC}=\widehat{xCy}\)
c)Cặp góc đồng vị là \(\widehat{ABC}\) và \(\widehat{xCy}\)

1) Vì a⊥d , b⊥d ⇒ a // b
⇒\(\widehat{A_1}=\widehat{B}=80^o\) (ở vị trí so le trong)
⇒\(\widehat{A_3}=\widehat{B}=80^o\)(ở vị trí đồng vị)
Do \(\widehat{A_2}+\widehat{B}=180^o\)
(hai góc trong cùng phía)
Thay số:\(\widehat{A_2}+80^o=180^o\)
⇒\(\widehat{A_2}=100^o\)
\(a,\left(x+3\right)^3-\left(x-1\right)^3=0\\ \Leftrightarrow\left(x^3+9x^2+27x+27\right)-\left(x^3-3x^2+3x-1\right)=0\\ \Leftrightarrow x^3+9x^2+27x+27-x^3+3x^2-3x+1=0\)
\(\Leftrightarrow12x^2+24x+28=0\\ \Leftrightarrow3x^2+6x+7=0\\ \Leftrightarrow9x^2+18x+21=0\\ \Leftrightarrow\left(3x\right)^2+2.3.3x+3^2+12=0\\ \Leftrightarrow\left(3x+3\right)^2+12=0\)
VÌ \(\left(3x+3\right)^2\ge0;12>0\Rightarrow\left(3x+3\right)^2+12>0\)
Vậy phương trình có tập nghiệm \(S=\varnothing\)
Tách nhỏ câu hỏi ra bạn