Cho hình thang cân ABCD (AB//CD) biết AB=26cm, AD=10cm và đường chéo AC vuông góc với cạnh bên BC. Tính diện tích của hình thang ABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 1 2017
2 đg chéo vuông góc vói nhau=>là hcn
dt hcn =dt ht cân
26x10=260 cm2
đ/s: 260 cm2
Ai tích mk mk sẽ tích lại
25 tháng 8 2023
Kẻ CH,DK lần lượt vuông góc AB
ΔCAB vuông tại C
=>CA^2+CB^2=AB^2
=>CA^2+10^2=26^2
=>CA=24cm
ΔCAB vuông tại C có CH là đường cao
nên CH*AB=CA*CB
=>CH*26=10*24=240
=>CH=120/13(cm)
ΔCHB vuông tại H
=>HB^2+CH^2=CB^2
=>HB^2=10^2-(120/13)^2=2500/169(cm)
=>HB=50/13(cm)
Xét ΔDKA vuông tại K và ΔCHB vuông tại H có
DA=CB
góc DAK=góc CBH
=>ΔDKA=ΔCHB
=>KA=HB=50/13cm
KH=AB-AK-HB
=26-50/13*2=238/13(cm)
Xét tứ giác KDCH có
DC//KH
DK//CH
Do đó: KDCH là hình bình hành
=>DC=KH=238/13(cm)
S ABCD=1/2*(DC+AB)*CH
=1/2(238/13+26)*120/13
=34560/169(cm2)
DD
Đoàn Đức Hà
Giáo viên
6 tháng 7 2021
Xét tam giác \(ABD\)vuông tại \(A\):
\(BD^2=AB^2+AD^2\)(định lí Pythagore)
\(=4^2+10^2=116\)
\(\Rightarrow BD=\sqrt{116}=2\sqrt{29}\left(cm\right)\)
Lấy \(E\)thuộc \(CD\)sao cho \(AE\perp AC\)
Suy ra \(ABDE\)là hình bình hành.
\(AE=BD=2\sqrt{29}\left(cm\right),DE=AB=4\left(cm\right)\).
Xét tam giác \(AEC\)vuông tại \(A\)đường cao \(AD\):
\(\frac{1}{AD^2}=\frac{1}{AE^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AC^2}=\frac{1}{AD^2}-\frac{1}{AE^2}=\frac{1}{100}-\frac{1}{116}=\frac{1}{715}\)
\(\Rightarrow AC=\sqrt{715}\left(cm\right)\)
\(AE^2=ED.EC\Leftrightarrow EC=\frac{AE^2}{ED}=\frac{116}{4}=29\left(cm\right)\)suy ra \(DC=25\left(cm\right)\)
Hạ \(BH\perp CD\).
\(BC^2=HC^2+BH^2=21^2+10^2=541\Rightarrow BC=\sqrt{541}\left(cm\right)\)
\(S_{ABCD}=\left(AB+CD\right)\div2\times AD=\frac{4+25}{2}\times10=145\left(cm^2\right)\)
CM
10 tháng 1 2018
a) DDBC vuông có B C D ^ = 2 B D C ^ nên A D C ^ = B C D ^ = 60 0 và D A B ^ = C B A ^ = 120 0
b) Tính được DC = 2.BC = 12cm, suy ra PABCD = 30cm.
Hạ đường cao BK, ta có BK = 3 3 c m .
Vậy SABCD = 27 3 c m 2
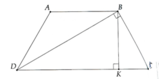
Gửi bạn lời giải. Có gì sai sót thì bạn góp ý nhé!
Kẻ \(\)$\(CH \perp AB\)$ tại H, $\(DK \perp AB\)$ tại K.
Áp dụng định lí Pytago vào tam giác ABC vuông tại C, ta có:
$\(AC^2=AB^2-BC^2=26^2-10^2=576\)$
Áp dụng hệ thức lượng vào tam giác ABC vuông tại C với đường cao CH, ta có:
$\(\dfrac{1}{CH^2}=\dfrac{1}{DK^2}=\dfrac{1}{AC^2}+\dfrac{1}{BC^2}=\dfrac{1}{100}+\dfrac{1}{576}=\dfrac{169}{14400}\)$ (do ABCD là hình thang cân)
⇒ $\(CH^2=DK^2=\dfrac{14400}{169}\)$
⇒ $\(CH=DK=\dfrac{120}{13}\)$
Áp dụng định lí Pytago vào tam giác CHB vuông tại H và tam giác AKD vuông tại K có:
$\(BH^2=AK^2=10^2-\dfrac{14400}{169}=\dfrac{2500}{169}\)$ ⇒ $\(BH=AK=\dfrac{50}{13}cm\)$ Ta có: $\(AB=AK+HK+BH=AK+CD+HK\)$ ⇒ $\(CD=AB-AK-HK=26-\dfrac{100}{13}=\dfrac{238}{13}\)$
Ta có: $\({S}_{ABCD}=\dfrac{(AB+CD).AH}{2}=\dfrac{(26+\dfrac{238}{13}).\dfrac{120}{13}}{2}=\dfrac{34560}{169} cm^2\)$