tìm a và b để số 86a43b chia hết cho cả
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8D
1
DV
1
10 tháng 11 2023
b: Đặt \(A=\overline{5a43b}\)
A chia hết cho 2 và 5 nên A có tận cùng là 0
=>b=0
=>\(A=\overline{5a430}\)
A chia hết cho 9
=>5+a+4+3+0 chia hết cho 9
=>a+12 chia hết cho 9
=>a=6
=>Số cần tìm là 56430
c: Đặt \(B=\overline{735a2b}\)
B chia hết cho 5 và không chia hết cho 2 nên b=5
=>\(B=\overline{735a25}\)
B chia hết cho 9
=>7+3+5+a+2+5 chia hết cho 9
=>a+22 chia hết cho 9
=>a=5
Vậy: Số cần tìm là 735525
d: Đặt \(C=\overline{5a27b}\)
C chia hết cho 2 và 5 nên C có tận cùng là 0
=>b=0
=>\(C=\overline{5a270}\)
C chia hết cho 9
=>5+a+2+7+0 chia hết cho 9
=>a+14 chia hết cho 9
=>a=4
Vậy: Số cần tìm là 54270
e: Đặt \(D=\overline{7a142b}\)
Vì D chia hết cho cả 2 và 5 nên D có tận cùng là 0
=>b=0
=>\(D=\overline{7a1420}\)
D chia hết cho 9
=>7+a+1+4+2+0 chia hết cho 9
=>a+14 chia hết cho 9
=>a=4
=>Số cần tìm là 741420
g: \(X=\overline{40ab}\)
X chia hết cho 2 và 5 nên b=0
=>\(X=\overline{40a0}\)
X chia hết cho 3
=>4+a+0+0 chia hết cho 3
=>a+4 chia hết cho 3
=>\(a\in\left\{2;5;8\right\}\)
M
24 tháng 8 2023
Để tìm các chữ số a và b thỏa mãn các điều kiện đã cho, ta sẽ kiểm tra từng trường hợp.
a. Để A = 3ab chia hết cho cả 2, 5, 3, 9, ta xét điều kiện chia hết cho 2 và chia hết cho 5:
Điều kiện chia hết cho 2: a phải là số chẵn.Điều kiện chia hết cho 5: b phải là 5 hoặc 0.Vậy, các cặp số (a, b) thỏa mãn là (2, 5) và (2, 0).
b. Để B = a72b chia hết cho cả 2, 5, 3, 9, ta xét điều kiện chia hết cho 2 và chia hết cho 5:
Điều kiện chia hết cho 2: b phải là số chẵn.Điều kiện chia hết cho 5: a + b = 7 + 2 + b chia hết cho 5. Vậy b = 3 hoặc 8.Vậy, các cặp số (a, b) thỏa mãn là (3, 3) và (8, 8).
c. Để C = 10a5b chia hết cho 45, ta xét điều kiện chia hết cho 45:
Điều kiện chia hết cho 45: tổng các chữ số của C chia hết cho 9 và C chia hết cho 5. Tổng các chữ số của C là 1 + 0 + a + 5 + b = 6 + a + b chia hết cho 9. Vậy a + b = 3 hoặc 12.Với a = 3, ta có b = 0. Với a = 1, ta có b = 11.
Vậy, các cặp số (a, b) thỏa mãn là (3, 0) và (1, 11).
d. Để D = 26a3b chia hết cho 5 và 18, ta xét điều kiện chia hết cho 5 và chia hết cho 18:
Điều kiện chia hết cho 5: b = 5 hoặc 0.Điều kiện chia hết cho 18: tổng các chữ số của D chia hết cho 9 và D chia hết cho 2. Tổng các chữ số của D là 2 + 6 + a + 3 + b = 11 + a + b chia hết cho 9. Vậy a + b = 7 hoặc 16.Với a = 1, ta có b = 6. Với a = 6, ta có b = 10.
Vậy, các cặp số (a, b) thỏa mãn là (1, 6) và (6, 10).
Tóm lại, các cặp số (a, b) thỏa mãn các điều kiện đã cho là: (2, 5), (2, 0), (3, 3), (8, 8), (3, 0), (1, 11), (1, 6) và (6, 10).
24 tháng 8 2023
a: A chia hết cho 2 và 5
=>b=0
A chia hết cho 9
=>3+a+0 chia hết cho 9
=>a=6
b: B chia hết cho 2 và 5
=>b=0
B chia hết cho 9
=>a+7+2+0 chia hết cho 9
=>a=0(loại) hoặc a=9(nhận)
c: C chia hết cho 45
=>C chia hết cho 5 và C chia hết cho 9
=>b=0 hoặc b=5
TH1: b=0
C chia hết cho 9
=>1+0+a+5+0 chia hết cho 9
=>a+6 chia hết cho 9
=>a=3
TH2: b=5
C chia hết cho 9
=>1+0+a+5+5 chia hết cho 9
=>a=7
d: D chia hết cho 5 và 18
=>D chia hết cho 2;5;9
=>b=0
D chia hết cho 9
=>2+6+a+3+0 chia hết cho 9
=>a=7
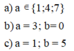
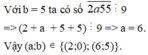
chia hết cho cả gì thế !??
TL
Sai Đề
HT