Tính \(\dfrac{7}{2x^2yz}+\dfrac{5}{3xy^3}\) Ai giúp thằng ngu này vs còn 5p ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 5 2017
Nhóm 1:-5x\(^2\)yz;\(\dfrac{2}{3}\)x\(^2\)yz
Nhóm 2:3xy\(^2\)z;-\(\dfrac{2}{3}\)xy\(^2\)z
Nhóm 3:10x\(^2\)y\(^2\)z;\(\dfrac{5}{7}\)x\(^2\)y\(^2\)z
15 tháng 12 2020
Ta có:
\(\dfrac{1}{x-y}+\dfrac{3xy}{y^3-x^3}+\dfrac{x-y}{x^2+xy+y^2}\\ =\dfrac{x^2+xy+y^2-3xy+\left(x-y\right)^2}{x^3-y^3}\\ =\dfrac{2\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\\ =\dfrac{2\left(x-y\right)}{x^2+xy+y^2}\)
15 tháng 12 2020
\(\dfrac{1}{x-y}+\dfrac{3xy}{y^3-x^3}+\dfrac{x-y}{x^2+xy+y^2}\) \(=\dfrac{x^2+xy+y^2}{x^3-y^3}-\dfrac{3xy}{x^3-y^3}+\dfrac{\left(x-y\right)^2}{x^3-y^3}\)
\(=\dfrac{x^2+xy+y^2-3xy+x^2-2xy+y^2}{x^3-y^3}\)
\(=\dfrac{2x^2+2y^2-4xy}{x^3-y^3}\)
\(=\dfrac{2x^2-2xy-2xy+2y^2}{x^3-y^3}\)
\(=\dfrac{2x\left(x-y\right)-2y\left(x-y\right)}{x^3-y^3}\)
\(=\dfrac{\left(2x-2y\right)\left(x-y\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2x-2y}{x^2+xy+y^2}\)
H
31 tháng 5 2018
Giải:
a) \(2x^2yz\left(-3xy^3z\right)=-6x^3y^4z^2\)
Bậc của đơn thức: \(3+4+2=9\)
b) \(\left(-12xyz\right)\left(\dfrac{-4}{3}x^2yz^3\right)y=16x^3y^3z^4\)
Bậc của đơn thức: \(3+3+4=10\)
c) \(-2x^2y\left(-3xy^2\right)^3=-2x^2y\left(-27x^3y^6\right)=54x^5y^7\)
Bậc của đơn thức: \(5+7=12\)
d) \(12\dfrac{1}{2}x^4\left(-\dfrac{2}{5}x^3y\right)^2=6x^4\left(\dfrac{4}{25}x^6y^2\right)=\dfrac{24}{25}x^{10}y^2\)
Bậc của đơn thức: \(10+2=12\)
31 tháng 5 2018
\(a,2x^2yz\left(-3xy^3z\right)=-6x^3y^4z^2\)
Bậc của đơn thức là 9
\(b,\left(-12xyz\right)\left(-\dfrac{4}{3}x^2yz^3\right)y=16x^3y^3z^4\)
Bậc của đơn thức: 10
\(c,-2x^2y\left(-3xy^2\right)^3\)
\(-2x^2y.\left(-27\right)x^3y^6=54x^5y^7\)
Bậc của đơn thức: 12
\(d,12\dfrac{1}{2}x^4\left(-\dfrac{2}{5}x^3y\right)^2\)
\(=12\dfrac{1}{2}x^4\cdot\dfrac{4}{25}x^6y^2=2x^{10}y^2\)
Bậc của đơn thức : 12
Q
2
11 tháng 10 2021
a) \(\dfrac{2x+3}{24}=\dfrac{3x-1}{32}\)
\(\Rightarrow32\left(2x+3\right)=24\left(3x-1\right)\)
\(\Rightarrow64x+96=72x-24\)
\(\Rightarrow8x=120\Rightarrow x=15\)
b) \(\dfrac{13x-2}{2x+5}=\dfrac{76}{17}\)
\(\Rightarrow17\left(13x-2\right)=76\left(2x+5\right)\)
\(\Rightarrow221x-34=152x+380\)
\(\Rightarrow69x=414\Rightarrow x=6\)
17 tháng 1 2023
\(1,\dfrac{4x-3}{x-5}=\dfrac{29}{3}\left(ĐKXĐ:x\ne5\right)\)
\(\Rightarrow3\left(4x-3\right)=29\left(x-5\right)\)
\(\Leftrightarrow12x-9=29x-145\)
\(\Leftrightarrow12x-9-29x+145=0\)
\(\Leftrightarrow-17x+136=0\)
\(\Leftrightarrow-17x=-136\)
\(\Leftrightarrow x=8\left(tm\right)\)
Vậy \(S=\left\{8\right\}\)
\(2,\dfrac{2x-1}{5-3x}=2\left(ĐKXĐ:x\ne\dfrac{5}{3}\right)\)
\(\Rightarrow2x-1=2\left(5-3x\right)\)
\(\Leftrightarrow2x-1=10-6x\)
\(\Leftrightarrow2x-1-10+6x=0\)
\(\Leftrightarrow8x-11=0\)
\(\Leftrightarrow8x=11\)
\(\Leftrightarrow x=\dfrac{11}{8}\left(tm\right)\)
Vậy \(S=\left\{\dfrac{11}{8}\right\}\)
\(3,\dfrac{4x-5}{x-1}=2+\dfrac{x}{x-1}\left(ĐKXĐ:x\ne1\right)\)
\(\Leftrightarrow\dfrac{4x-5}{x-1}=\dfrac{2\left(x-1\right)}{x-1}+\dfrac{x}{x-1}\)
\(\Leftrightarrow\dfrac{4x-5}{x-1}=\dfrac{2x-2}{x-1}+\dfrac{x}{x-1}\)
\(\Leftrightarrow\dfrac{4x-5}{x-1}=\dfrac{3x-2}{x-1}\)
\(\Rightarrow4x-5=3x-2\)
\(\Leftrightarrow4x-5-3x+2=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\left(tm\right)\)
Vậy \(S=\left\{3\right\}\)
\(4,\dfrac{2x+5}{2x}-\dfrac{x}{x+5}=0\left(ĐKXĐ:x\ne\dfrac{1}{2};x\ne-5\right)\)
\(\Leftrightarrow\dfrac{\left(2x+5\right)\left(x+5\right)}{2x\left(x+5\right)}-\dfrac{2x^2}{2x\left(x+5\right)}=0\)
\(\Leftrightarrow\dfrac{2x^2+15x+25}{2x\left(x+5\right)}-\dfrac{2x^2}{2x\left(x+5\right)}=0\)
\(\Leftrightarrow\dfrac{15x+25}{2x\left(x+5\right)}=0\)
\(\Rightarrow15x+25=0\)
\(\Leftrightarrow15x=-25\)
\(\Leftrightarrow x=\dfrac{-5}{3}\left(tm\right)\)
Vậy \(S=\left\{\dfrac{-5}{3}\right\}\)
Y
17 tháng 1 2023
\(1,\dfrac{4x-3}{x-5}=\dfrac{29}{3}\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-29\left(x-5\right)}{3\left(x-5\right)}=0\)
\(\Leftrightarrow12x-9-29x+145=0\)
\(\Leftrightarrow-17x=-136\)
\(\Leftrightarrow x=8\)
\(2,\dfrac{2x-1}{5-3x}=2\)
\(\Leftrightarrow\dfrac{2x-1-2\left(5-3x\right)}{5-3x}=0\)
\(\Leftrightarrow2x-1-10+6x=0\)
\(\Leftrightarrow8x=11\)
\(\Leftrightarrow x=\dfrac{11}{8}\)
\(3,\dfrac{4x-5}{x-1}=2+\dfrac{x}{x-1}\)
\(\Leftrightarrow\dfrac{4x-5-2\left(x-1-x\right)}{x-1}=0\)
\(\Leftrightarrow4x-5-2x+2+2x=0\)
\(\Leftrightarrow4x=3\)
\(\Leftrightarrow x=\dfrac{3}{4}\)
\(4,\dfrac{2x+5}{2x}-\dfrac{x}{x+5}=0\)
\(\Leftrightarrow\dfrac{\left(2x+5\right)\left(x+5\right)-2x^2}{2x\left(x+5\right)}=0\)
\(\Leftrightarrow2x^2+10x+5x+25-2x^2=0\)
\(\Leftrightarrow15x=-25\)
\(\Leftrightarrow x=-\dfrac{5}{3}\)
18 tháng 10 2021
b: \(B=\dfrac{3y+5}{y-1}-\dfrac{-y^2-4y}{y-1}+\dfrac{y^2+y+7}{y-1}\)
\(=\dfrac{3y+5+y^2+4y+y^2+y+7}{y-1}\)
\(=\dfrac{2y^2+8y+12}{y-1}\)
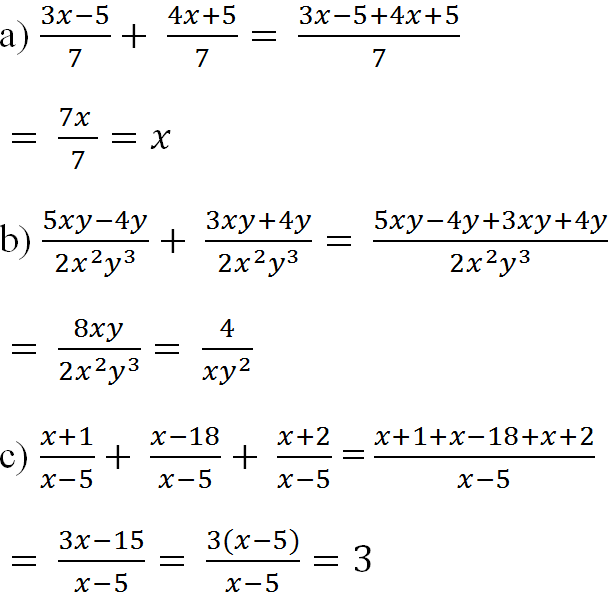
giúp vs ạ
\(=\dfrac{21y^2+10xz}{6x^2y^3z}\)