1.cho hàm số y=(2m-2/2) x+2n-1(d) và hàm số y=4x+2-n(d') a) tìm điều kiện của m để (d) là hàm số bậc nhất b) tìm điều kiện của m để (d) là hàm số đồng biến c) hàm số (d') đồng biến hay nghịch biến tại sao? d) vẽ đồ thị hàm số (d') khi n=4 e) tìm điều kiện của m, n để (d) // (d') 2. Cho 2 hàm số y= -x + 6 =y=3x -6 a) vẽ 2 hàm số trên cùng hệ trục tọa độ b) tìm tọa độ giao điểm của 2 hàm số trên Ai giúp mình với, mình cần gấp ạ!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Để hàm số là hàm số bậc nhất thì 2m-3<>0
hay m<>3/2
b: Để hàm số đồng biến thì 2m-3>0
hay m>3/2
Để hàm số nghịch biến thì 2m-3<0
hay m<3/2

a.
Hàm là hàm số bậc nhất khi:
\(2m-1\ne0\Leftrightarrow m\ne\dfrac{1}{2}\)
b.
Hàm đồng biến trên R khi:
\(2m-1>0\Leftrightarrow m>\dfrac{1}{2}\)
a) Để hàm số là hàm số bậc nhất thì \(2m-1\ne0\)
hay \(m\ne\dfrac{1}{2}\)
b) Để hàm số đồng biến thì 2m-1>0
hay \(m>\dfrac{1}{2}\)

a> gọi y=(m-2)x+n là (d)
để (d) là hsbn thì m khác 2, với mọi n thuộc R
b> hàm số đồng biến khi m>2
nghịch biến khi m<2
c> điều kiện để (d) // (d'): y=2x-1 <=> m-2=2 <=>m=4
và n khác -1
vậy để (d) // (d') <=> m=4, m khác 2, n khác -1
d> điều kiện để (d) cắt (d''): y=-3x+2 <=> m-2=-3 <=> m khác -1
vậy để (d) cắt (d'') <=> m khác 2, m khác -1
e> để (d) trùng (d'''): y=3x-2 <=> m-2=3 <=> m=5
và n = -2
vậy để d//d''' <=> m khác 2, m=5, n=-2
f> vì d đi qua A(1;2) => 2=m-2+n <=> m+n=4 (1). vì d đi qua B(3;4) => 4=3m-6+n <=> 3m+n = 10 (2)
lấy (2) trừ (1) <=> 2m=6 <=> m= 3 => n=1

a: Để hàm số nghịch biên thì m-2<0
=>m<2
b: Thay x=3 và y=0 vào (d), ta đc:
3(m-2)+m+3=0
=>3m-6+m+3=0
=>4m-3=0
=>m=3/4
c: Tọa độ giao điểm là
2x-1=-x+2 và y=-x+2
=>x=1 và y=1
Thay x=1 và y=1 vào (d), ta được:
m-2+m+3=1
=>2m+1=1
=>m=0

1: (D): y=(m-2)x+1
(D'): \(y=m^2x-2x+m=x\left(m^2-2\right)+m\)
Để (D) là hàm số bậc nhất thì m-2<>0
=>m<>2
Để (D): y=(m-2)x+1 đồng biến trên R thì m-2>0
=>m>2
Để (D): y=(m-2)x+1 nghịch biến trên R thì m-2<0
=>m<2
2: Để (D)//(D') thì \(\left\{{}\begin{matrix}m^2-2=m-2\\m< >1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2-m=0\\m< >1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\left(m-1\right)=0\\m< >1\end{matrix}\right.\)
=>m=0
3:
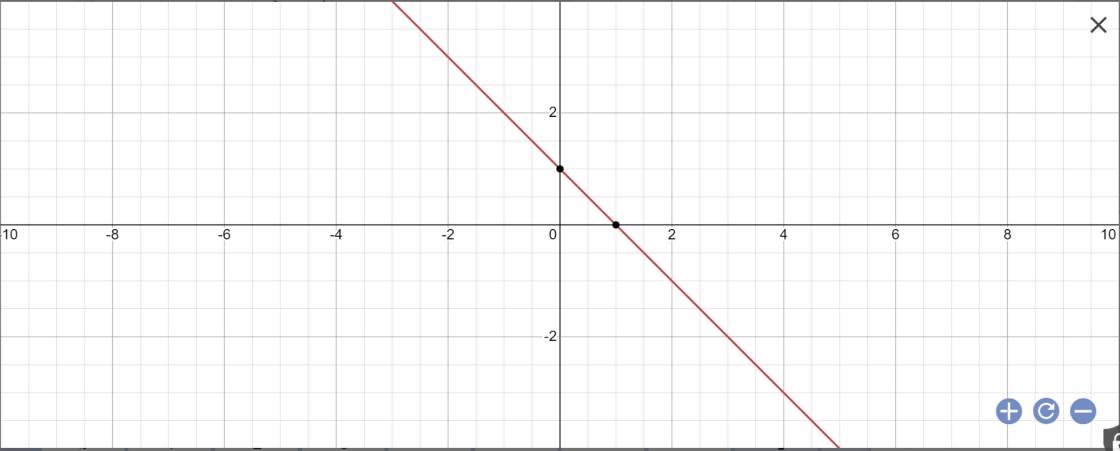
a: Khi m=0 thì (D): y=(0-2)x+1=-x+1
b: Gọi \(\alpha\) là góc tạo bởi (D) với trục Ox
Ta có: a=-1
nên \(tan\left(180^0-\alpha\right)=-1\)
=>\(180-\alpha=135^0\)
=>\(\alpha=45^0\)
4:
Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}2x-8=-x+1\\y=2x-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=9\\y=2x-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2\cdot3-8=-2\end{matrix}\right.\)
Thay x=3 và y=-2 vào (D), ta được:
\(3\left(m-2\right)+1=-2\)
=>3(m-2)=-3
=>m-2=-1
=>m=1
5: Để (D) cắt (D') tại một điểm trên trục hoành thì
\(\left\{{}\begin{matrix}m-2< >m^2-2\\-\dfrac{1}{m-2}=\dfrac{-m}{m^2-2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2-m\ne0\\\dfrac{1}{m-2}=\dfrac{m}{m^2-2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\left(m-1\right)\ne0\\m^2-2=m^2-2m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\notin\left\{0;1\right\}\\-2m=-2\end{matrix}\right.\)
=>\(m\in\varnothing\)
6: (D): y=(m-2)x+1
=>y=mx-2x+1
Điểm mà (D) luôn đi qua có tọa độ là:
\(\left\{{}\begin{matrix}x=0\\y=-2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-2\cdot0+1=1\end{matrix}\right.\)

Hàm nghịch biến trên R khi và chỉ khi:
\(m-2< 0\)
\(\Rightarrow m< 2\)

a: Để hàm số nghịch biến trên R thì m-2<0
=>m<2
b: Thay x=-3 và y=0 vào (d), ta được:
-3(m-2)+m+3=0
=>-3m+6+m+3=0
=>-2m+9=0
=>-2m=-9
=>\(m=\dfrac{9}{2}\)
c: Tọa độ giao điểm của y=-x+2 và y=2x-1 là:
\(\left\{{}\begin{matrix}2x-1=-x+2\\y=-x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=3\\y=-x+2\end{matrix}\right.\)
=>x=1 và y=-1+2=1
Thay x=1 và y=1 vào (d), ta được:
m+2+m+3=1
=>2m+5=1
=>2m=-4
=>m=-4/2=-2
Bài 1:
a: Để (d) là hàm số bậc nhất thì 2m-2<>0
hay m<>1
b: Để (d) là hàm số đồng biến thì 2m-2>0
hay m>1
c: Hàm số (d') đồng biến vì a=4>0
Bài 2:
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-x+6=3x-6\\y=-x+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=3\end{matrix}\right.\)