Gieo một con xúc xắc 3 lần. Tính xác suất để tổng số chấm xuất hiện ở 3 lần gieo là một số chẵn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
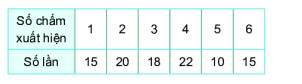
Các số chẵn là 2;4;6
Số lần được 2 là 20, số lần được 4 là 22, số lần được 6 là 15.
Số lần được số chẵn là: 20+22+15=57
Xác suất thực nghiệm của sự kiện “Số chấm xuất hiện là số chẵn” là:\(\frac{{57}}{{100}} = 57\% \)
b.
Các số lớn hơn 2 là 3;4;5;6
Số lần được 3 là 18, số lần được 4 là 22, số lần được 5 là 10, số lần được 6 là 15.
Số lần được số lớn hơn 2 là: 18+22+10+15=65
Xác suất thực nghiệm của sự kiện “Số chấm xuất hiện lớn hơn 2” là:\(\frac{{65}}{{100}} = 65\% \)

a: A={(1;1); (1;2); ...; (1;6)}
=>n(A)=6
P(A)=6/36=1/6
b: B={(1;4); (2;3); (3;2); (4;1)}
=>P(B)=4/36=1/9
c: C={(3;1); (4;2); (5;3); (6;4)}
=>P(C)=4/36=1/9
d: D={(1;3); (1;5); (1;1); (3;5); (3;1); (3;3); (5;3); (5;1); (5;5)}
=>P(D)=9/36=1/4


Có thể là 2 lần chẵn 1 lần lẻ hoặc cả 3 lần đều chẵn
TH1: 2 chẵn, 1 lẻ
=>Có \(C^1_3\cdot C^1_3\cdot C^1_3=27\left(cách\right)\)
TH2: 3 lần đều chẵn
=>Có \(C^1_3\cdot C^1_3\cdot C^1_3=27\left(cách\right)\)
=>Có 27+27=54 cách
n(omega)=6*6*6=216
=>P=54/216=1/4

Không gian mẫu là tập hợp số chấm xuất hiện khi gieo con xúc xắc hai lần liên tiếp khi đó \(n\left( \Omega \right) = 6.6 = 36\)
A = {(1; 1); (1; 2); (1; 3); (1; 4); (1; 5); (1; 6)} \( \Rightarrow P\left( A \right) = \frac{6}{{36}} = \frac{1}{6}\)
B = {(1; 2); (2; 2); (3; 2); (4; 2); (5; 2); (6; 2)} \( \Rightarrow P\left( B \right) = \frac{6}{{36}} = \frac{1}{6}\)
C = {(2; 6); (3; 5); (4; 4); (5; 3); (6; 2)} \( \Rightarrow P\left( C \right) = \frac{5}{{36}}\)
D = {(1; 6); (2; 5); (3; 4); (4; 3); (5; 2); (6; 1)} \( \Rightarrow P\left( D \right) = \frac{6}{{36}} = \frac{1}{6}\)
Do đó
\(P\left( A \right).P\left( C \right) = \frac{1}{6}.\frac{5}{{36}} = \frac{5}{{216}};P\left( B \right).P\left( C \right) = \frac{1}{6}.\frac{5}{{36}} = \frac{5}{{216}};P\left( C \right).P\left( D \right) = \frac{5}{{36}}.\frac{1}{6} = \frac{5}{{216}}\)
Mặt khác
AC = \(\emptyset \Rightarrow P\left( {AC} \right) = 0\)
BC = {(6; 2)} \( \Rightarrow P\left( {BC} \right) = \frac{1}{{36}}\)
CD = \(\emptyset \Rightarrow P\left( {CD} \right) = 0\)
Khi đó \(P\left( {AC} \right) \ne P\left( A \right).P\left( C \right);P\left( {BC} \right) \ne P\left( B \right).P\left( C \right);P\left( {CD} \right) \ne P\left( C \right).P\left( D \right)\)
Vậy các cặp biến cố A và C; B và C, C và D không độc lập.

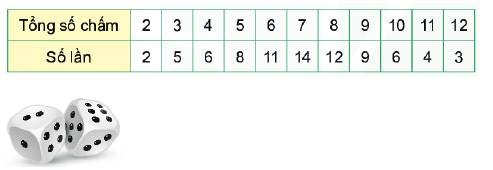
Ta có 14 lần gieo được 7 chấm, 12 lần gieo được 8 chấm, 9 lần gieo được 9 chấm, 6 lần gieo được 10 chấm, 4 lần gieo được 11 chấm và 3 lần gieo được 12 chấm.
Số lần gieo được 7 chấm trở lên là 14 + 12 + 9 + 6 + 4 + 3 = 48 lần.
Do đó số lần An thắng là 48 lần.
Xác xuất thực nghiệm của sự kiện “An thắng” là:\(\dfrac{{48}}{{80}} = \dfrac{3}{5} = \dfrac{3}{5}.100\% = 60\% \)

a: n(omega)=36
A={(1;5); (2;5); (3;5); (4;5); (5;5); (6;5)}
=>n(A)=6
=>P(A)=6/36=1/6
b: B={(1;6); (2;5); (3;4); (4;3); (5;2); (6;1)}
=>n(B)=6
=>P(B)=1/6
d: D={(2;1); (2;2); ...; (2;6); (3;1); (3;2); ...;(3;6);(5;1); (5;2);...;(5;6)}
=>P(D)=18/36=1/2

a: n(omega)=6
n(A)=3
=>P(A)=3/6=1/2
b: n(B)=5
=>P(B)=5/6