( y - 1/2 ) +(y - 1/6 ) + (y - 1/12 ) + .......+ ( y - 1/90 ) = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(y - 1/2) : (1/2 + 1/6 + 1/12 + ... + 1/90) = 1/3
(y - 1/2) : (1/1×2 + 1/2×3 + 1/3×4 + ... + 1/9×10) = 1/3
(y - 1/2) : (1 - 1/2 + 1/2 - 1/3 + 1/3 - 1/4 + ... + 1/9 - 1/10) = 1/3
(y - 1/2) : (1 - 1/10) = 1/3
(y - 1/2) : 9/10 = 1/3
y - 1/2 = 1/3 × 9/10
y - 1/2 = 3/10
y = 3/10 + 1/2
y = 3/10 + 5/10
y =8/10 = 4/5

(y - \(\dfrac{1}{2}\)) : \(\left(\dfrac{1}{2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{9.10}\right)\)= \(\dfrac{1}{3}\)
(y\(-\dfrac{1}{2}\)): \(\left(\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{9}-\dfrac{1}{10}\right)\)= \(\dfrac{1}{3}\)
\(\left(y-\dfrac{1}{2}\right):\left(\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{10}\right)=\dfrac{1}{3}\)
\(\left(y-\dfrac{1}{2}\right):\dfrac{3}{10}=\dfrac{1}{3}\)
\(\left(y-\dfrac{1}{2}\right)=\dfrac{1}{10}\)
y = \(\dfrac{3}{5}\)

Đặt \(A=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+....+\frac{1}{90}\)
\(A=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+....+\frac{1}{9.10}\)
\(A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+....+\frac{1}{9}-\frac{1}{10}\)
\(A=1-\frac{1}{10}\)
\(A=\frac{9}{10}\)
\(=>\left[y-\frac{1}{2}\right]x\frac{9}{10}=\frac{1}{3}\)
\(y-\frac{1}{2}=\frac{1}{3}:\frac{9}{10}\)
\(y-\frac{1}{2}=\frac{10}{27}\)
\(=>y=\frac{10}{27}+\frac{1}{2}\)
\(y=\frac{20+27}{54}=\frac{47}{54}\)
Vậy \(y=\frac{47}{54}\)
Ủng hộ mk nha!!!

\(\left(y-\frac{1}{2}\right):\left(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{9.10}\right)=\frac{1}{3}\)
\(\Leftrightarrow\left(y-\frac{1}{2}\right):\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-...+\frac{1}{9}-\frac{1}{10}\right)=\frac{1}{3}\)
\(\Leftrightarrow\left(y-\frac{1}{3}\right):\left(1-\frac{1}{10}\right)=\frac{1}{3}\)
\(\Leftrightarrow\left(y-\frac{1}{2}\right):\frac{9}{10}=\frac{1}{3}\)
\(\Leftrightarrow\left(y-\frac{1}{2}\right)=\frac{3}{10}\)
\(\Leftrightarrow y=\frac{4}{5}\)

Ta có
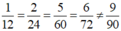
Do đó, hai đại lượng x và y không tỉ lệ thuận với nhau.

Do x và y là hai đại lượng tỉ lệ thuận và \(x_1,x_2\)là hai giá trị khác nhau của x;\(y_1,y_2\)là hai giá trị tương ứng của y nên
\(\frac{y_1}{y_2}=\frac{x_1}{x_2}=\frac{2y_1}{2y_2}=\frac{3x_1}{3x_2}=\frac{2y_1+3x_1}{2y_2+3x_2}\)
Vì \(x_2=-6,y_2=-3\)và \(2y_1+3x_1=24\)nên ta có :
\(\frac{y_1}{-3}=\frac{x_1}{-6}=\frac{2y_1+3x_1}{2\cdot\left(-3\right)+3\cdot\left(-6\right)}=\frac{24}{-24}=-1\)
=> \(y_1=\left(-1\right)\cdot\left(-3\right)=3;x_1=\left(-1\right)\cdot\left(-6\right)=6\)
=>( y - 1/2 )+( y - 1/6 )+...+( y- 1/90 ) = 1
=>y + y+.. + y - 1/2 - 1/6-...- 1/90 = 1
=>y + y+..+ y - 1/(1x2) - 1/(2x3) - 1/(3x4)-...- 1/(9x10) = 1
=> 9y -( 2-1)/(1x2) - (3-2)/(2x3)-...- (10-9)/(9x10) = 1
=>9y- 2/(1x2) + 1(1x2) - 3/(2x3) + 2/(2x3)-...- 10/(9x10) + 9(9x10) = 1
=> 9y- 1 + 1/2 - 1/2 + 1/3-...- 1/9 + 1/10 = 1
=>9y- 1 + 1/10 = 1
=> 9y- 9/10 =1
=>y=19/90
Vậy y=19/90
y=19/10