khi rút gọn câu cần chú ý điều gì ? ( mn giúp em vs ạ em cảm ơn nhiều lắm )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)
\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)
\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)
\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)
\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)
\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)
\(=\left(a-1\right)^2=a^2-2a+1\)





ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1-6\sqrt{x-1}+9}=0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(3-\sqrt{x-1}\right)^2}=0\)
\(\Leftrightarrow\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|=0\)
Do \(\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|\ge\left|\sqrt{x-1}-2+3-\sqrt{x-1}\right|=1>0\) với mọi x thuộc TXĐ
\(\Rightarrow\) Phương trình đã cho vô nghiệm

2b.
\(Q=\dfrac{cosx}{sinx}+\dfrac{sinx}{1+cosx}=\dfrac{cosx\left(1+cosx\right)+sin^2x}{sinx\left(1+cosx\right)}=\dfrac{cosx+cos^2x+sin^2x}{sinx\left(1+cosx\right)}=\dfrac{cosx+1}{sinx\left(1+cosx\right)}=\dfrac{1}{sinx}\)
4b.
\(\Delta\) có 1 vtpt là (3;-4)
Gọi d là đường thẳng qua M và vuông góc \(\Delta\Rightarrow d\) nhận (4;3) là 1 vtpt
Phương trình d:
\(4\left(x-4\right)+3\left(y+2\right)=0\Leftrightarrow4x+3y-10=0\)
H là giao điểm d và \(\Delta\) nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}3x-4y+5=0\\4x+3y-10=0\end{matrix}\right.\) \(\Rightarrow H\left(1;2\right)\)
 Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.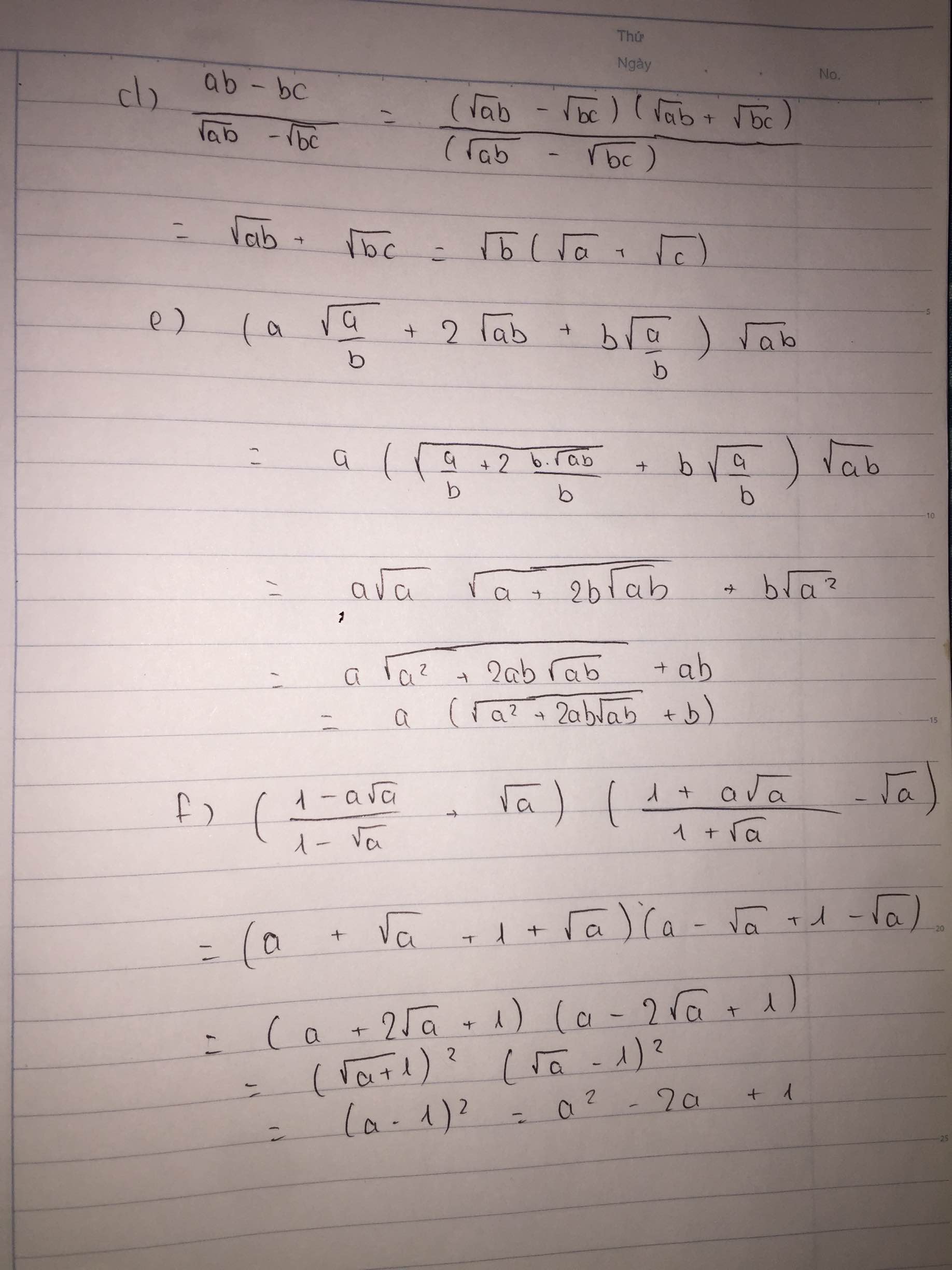
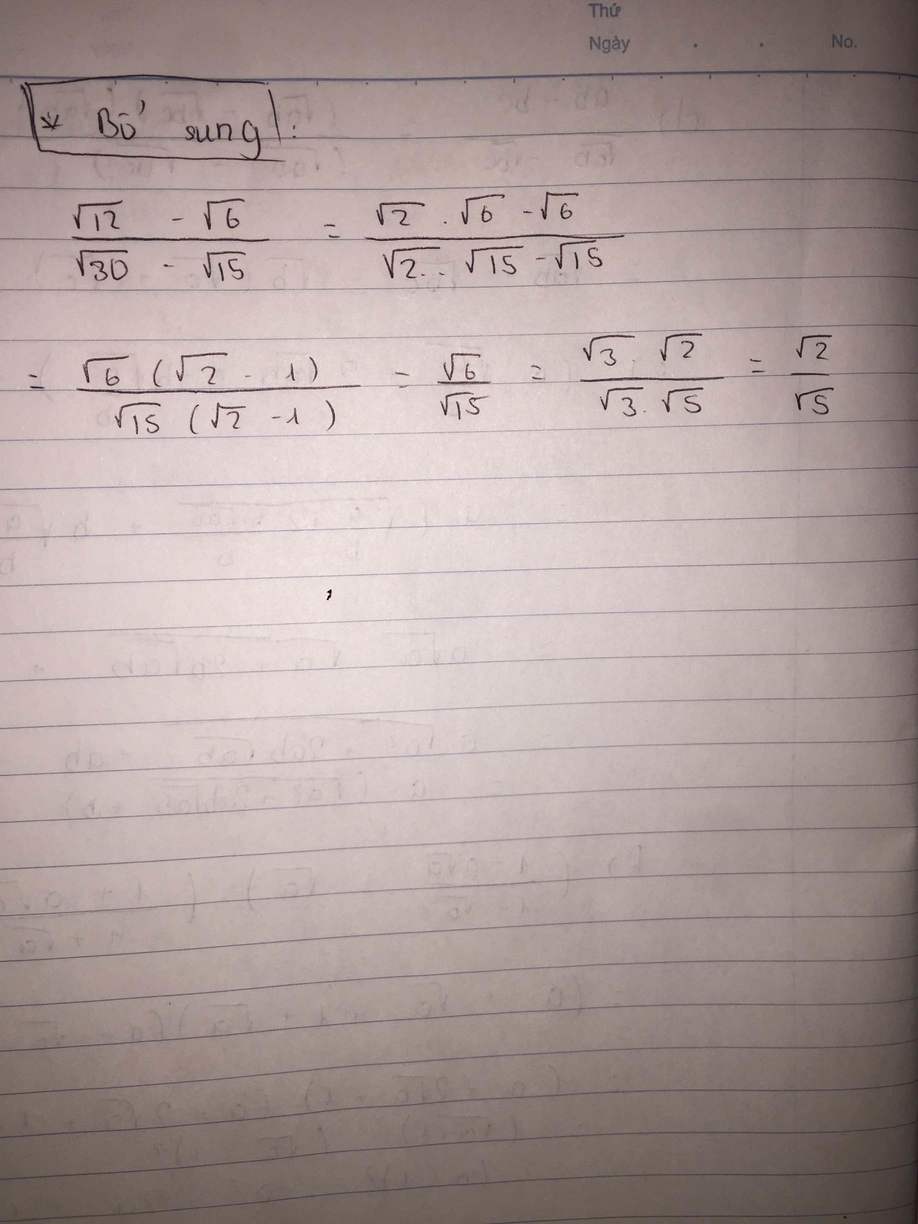
 gấp mn giúp em câu này vs ạ e gấp lắm mn giúp em vs em cảm ơn ạ
gấp mn giúp em câu này vs ạ e gấp lắm mn giúp em vs em cảm ơn ạ





Khi rút gọn câu cần chú ý :
+ Không quá lợi dụng việc rút gọn làm cho câu từ trở nên thô tục
+ Phải lễ phép trong câu rút gọn với người lớn tuổi
tham khảo: