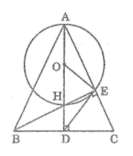
Cho \(\Delta ABC\) cân tại A, các đường cao AM và BN cắt nhau tại H. Chứng minh rằng MN là tiếp tuyến của đường tròn tâm O đường kính AH.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 5 2023
góc ONM=góc ONH+góc MNB
=góc OHN+góc MNB
=góc NBC+góc MHB=90độ
=>MN là tiếp tuyến của (O)
CM
16 tháng 9 2017
Ta có : OH = OE
Suy ra tam giác OHE cân tại O
Trong tam giác BDH ta có:
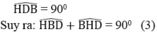
Từ (1), (2) và (3) suy ra:
Tam giác ABC cân tại A có AD ⊥ BC nên BD = CD
Tam giác BCE vuông tại E có ED là đường trung tuyến nên:
ED = DB = BC/2 (tính chất tam giác vuông)
Suy ra tam giác BDE cân tại D
Suy ra: DE ⊥ EO. Vậy DE là tiếp tuyến của đường tròn (O).
3 tháng 8 2018
a/ Xét \(\Delta AEH\)vuông tại E có:
EO là đường trung tuyến ( OA=OH )
\(\Rightarrow EO=\frac{1}{2}AH=OA=OH\)( tính chất đường trung tuyến trong tam giác vuông )
\(\Rightarrow E\)nằm trên đường tròn tâm O đường kính AH
b/ Xét \(\Delta OHE\)có:
OH=OE ( cmt )
\(\Rightarrow\Delta OHE\)cân tại O
\(\Rightarrow\widehat{OEH}=\widehat{OHE}\)( tính chất tam giác cân )
Mà: \(\widehat{BHD}=\widehat{OHE}\)( 2 góc đối đỉnh )
\(\Rightarrow\widehat{OEH}=\widehat{BHD}\left(=\widehat{OHE}\right)\)(1)
Xét \(\Delta ABC\)cân tại A có:
AD là đường cao ( gt )
\(\Rightarrow AD\)là đường trung tuyến
\(\Rightarrow BD=CD\)
Xét \(\Delta BEC\)vuông tại E có:
ED là đường trung tuyến ( BD=CD )
\(\Rightarrow ED=\frac{1}{2}BC=BD\)( tính chất đường trung tuyến trong tam giác vuông )
\(\Rightarrow\Delta BDE\)cân tại D
\(\Rightarrow\widehat{DEH}=\widehat{DBH}\)(2)
Từ (1) và (2) suy ra: \(\widehat{OEH}+\widehat{DEH}=\widehat{BHD}+\widehat{DBH}\)
Hay \(\widehat{OED}=90\)( \(\widehat{BHD}\)và \(\widehat{DBH}\)là 2 góc phụ nhau của \(\Delta BHD\)vuông tại D )
\(\Rightarrow DE\perp OE\)
Vậy DE là tiếp tuyến của đường tròn (O).
12 tháng 1 2023
a: Xét (I) có
ΔHMB nội tiếp
HB là đường kính
Do đó: ΔHMB vuông tại M
Xét (K) có
ΔCNH nội tiếp
HC là đường kính
Do đó; ΔCNH vuông tại N
Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
nên AMHN là hình chữ nhật
b: góc IMN=góc IMH+góc NMH
=góc IHM+góc NAH
=góc HAC+góc HCA=90 độ
=>NM là tiếp tuyến của (I)
góc KNM=góc KNH+góc MNH
=góc KHN+góc MAH
=góc HBA+góc HAB=90 độ
=>MN là tiếp tuyến của (K)
3 tháng 7 2023
a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
góc EAH+góc ACB=90 độ
góc EBC+góc ACB=90 độ
=>góc EAH=góc EBC
b: AK cắt EF tại M
AK cắt BC tại N
AH cắt (O) tại K
=>HM//AB và QN//AB
=>HM//QN
Gọi O là trung điểm AH, tam giác AHN vuông tại N nên N thuộc đường tròn đường kính AH
Do ABC cân tại A \(\Rightarrow\) AM là đường cao đồng thời là trung tuyến
\(\Rightarrow\) M là trung điểm BC
Trong tam giác vuông NBC, NM là trung tuyến ứng với cạnh huyền
\(\Rightarrow MN=MB=\dfrac{1}{2}BC\Rightarrow\Delta MNB\) cân tại M
\(\Rightarrow\widehat{MNB}=\widehat{MBN}\) (1)
Tương tự, trong tam giác vuông ANH, ta có: \(ON=OH=\dfrac{1}{2}AH\Rightarrow\widehat{ONH}=\widehat{OHN}\)
Mà \(\widehat{OHN}=\widehat{MHB}\) (đối đỉnh) \(\Rightarrow\widehat{ONH}=\widehat{MHB}\) (2)
Lại có tam giác HBM vuông tại M \(\Rightarrow\widehat{MHB}+\widehat{MBN}=90^0\) (3)
(1);(2);(3) \(\Rightarrow\widehat{ONH}+\widehat{MNB}=90^0\) hay \(MN\perp ON\)
\(\Rightarrow MN\) là tiếp tuyến của đường tròn đường kính AH