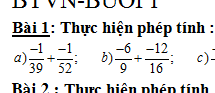plz somebody help me
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
somebody help me plz =))
14 tháng 11 2021
b, Gọi \(\left(d_3\right):y=ax+b\left(a\ne0\right)\) là đt cần tìm
\(P\left(1;3\right)\in\left(d_3\right)\Leftrightarrow a+b=3\left(1\right)\\ \left(d_3\right)\perp\left(d_1\right)\Leftrightarrow2a=-1\Leftrightarrow a=-\dfrac{1}{2}\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{2}\\b=3+\dfrac{1}{2}=\dfrac{7}{2}\end{matrix}\right.\)
Vậy đt cần tìm là \(y=-\dfrac{1}{2}x+\dfrac{7}{2}\)
c, Gọi \(\left(d\right):y=cx+d\left(c\ne0\right)\) là đt của (d)
\(\left(d\right)//Ox\Leftrightarrow d=y\\ C\left(0;2\right)\in\left(d\right)\Leftrightarrow d=2=y\\ \Leftrightarrow\left(d\right):y=2\)
PTHDGD của (d) và (d1) là \(2x=2\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow A\left(1;2\right)\Leftrightarrow OA=1\)
PTHDGD của (d) và (d2) là \(\dfrac{1}{2}x=2\Leftrightarrow x=4\Leftrightarrow y=2\Leftrightarrow B\left(4;2\right)\Leftrightarrow OB=4\)
\(AB=OA+OB=5\)
Gọi D là chân đường cao từ O tới AB
\(\Leftrightarrow OD=2\) (do \(D\in\left(d\right):y=2\))
Vậy \(S_{ABO}=\dfrac{1}{2}OD\cdot AB=5\left(đvdt\right)\)
AQ
1
AH
Akai Haruma
Giáo viên
26 tháng 2 2022
Lời giải:
$(y+2)(x^2+1)=2x^3+3x+1$
$\Leftrightarrow y+2=\frac{2x^3+3x+1}{x^2+1}$
\(=\frac{2x(x^2+1)+(x+1)}{x^2+1}=2x+\frac{x+1}{x^2+1}\)
$\Leftrightarrow y+2-2x=\frac{x+1}{x^2+1}$
$x,y$ nguyên nên $y+2-2x$ nguyên $\Leftrightarrow \frac{x+1}{x^2+1}$ nguyên
$\Leftrightarrow x+1\vdots x^2+1$
Khi đó có 2 TH xảy ra:
TH1: $x+1=0$
$\Leftrightarrow x=-1$
Thay vô pt ban đầu suy ra $y=-4$ (tm)
TH2: $x+1\neq 0$. Khi đó $x+1\vdots x^2+1$
$\Rightarrow x+1\geq x^2+1$
$\Leftrightarrow x^2-x\leq 0\Leftrightarrow x(x-1)\leq 0$
$\Leftrightarrow 0\leq x\leq 1$
Vì $x$ nguyên nên $x=0$ hoặc $x=1$. Thử vào pt ban đầu suy ra $(x,y)=(0,1), (1,3)$
Vậy.........
LN
3
4 tháng 9 2021
\(\left|2\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|4\overrightarrow{MB}-\overrightarrow{MC}\right|\)
⇔ \(\left|2\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|3\overrightarrow{MB}+\overrightarrow{CB}\right|\) (1)
Trên cạnh AB lấy O sao cho \(\dfrac{OA}{OB}=\dfrac{1}{2}\)
⇒ \(2\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{0}\)
Trên cạnh tia đối của tia BC lấy E sao cho \(\dfrac{EB}{BC}=\dfrac{1}{3}\)
⇒ \(3\overrightarrow{EB}+\overrightarrow{CB}=\overrightarrow{0}\)
Vậy (1) ⇒ \(\left|3\overrightarrow{MO}+2\overrightarrow{OA}+\overrightarrow{OB}\right|=\left|3\overrightarrow{ME}+3\overrightarrow{EB}+\overrightarrow{CB}\right|\)
⇒ 3MO = 3ME
⇒ MO = ME
⇒ M nằm trên đường trung trực của OE
help me, plz:(
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
d. G thuộc Ox nên \(G\left(2;0\right)\)
d qua G nên:
\(2\left(m^2-3m\right)+2m-5=0\)
\(\Leftrightarrow2m^2-4m-5=0\Rightarrow m=\dfrac{2\pm\sqrt{14}}{2}\)
b.
H thuộc Oy nên: \(H\left(0;3\right)\)
d qua H nên:
\(0\left(m^2-3m\right)+2m-5=3\)
\(\Rightarrow2m=8\Rightarrow m=4\)
14 tháng 9 2021
bài 1)
a)\(\dfrac{-1}{39}+\dfrac{-1}{52}\)
\(=\dfrac{-4}{156}+\dfrac{-3}{156}\)
\(=\dfrac{-7}{156}\)
b)\(\dfrac{-6}{9}+\dfrac{-12}{16}\)
\(=\dfrac{-96}{144}+\dfrac{-108}{144}\)
\(=\dfrac{-204}{144}\)
\(=\dfrac{-17}{12}\)
