trong mặt phẳng Oxy A(3,2) B(-5,4) và C(x,1) tìm x =3 để điểm a,b,c thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\overrightarrow{AB}=\left(-9;5\right)\)
\(\overrightarrow{AC}=\left(-\dfrac{9}{4};\dfrac{1}{2}\right)\)
Vì \(\overrightarrow{AB}=k\cdot\overrightarrow{AC}\) nên A,B,C thẳng hàng

Tham khảo:
a) Ta có: \(\overrightarrow {OA} = \left( {2;1} \right)\) ( do A(2; 1)) và \(\overrightarrow {OB} = \left( {3;3} \right)\) (do B (3; 3)).
Hai vectơ này không cùng phương (vì \(\frac{2}{3} \ne \frac{1}{3}\)).
Do đó các điểm O, A, B không cùng nằm trên một đường thẳng.
Vậy chúng không thẳng hàng.
b) Các điểm O, A, B không thẳng hàng nên OABM là một hình hành khi và chỉ khi \(\overrightarrow {OA} = \overrightarrow {MB} \).
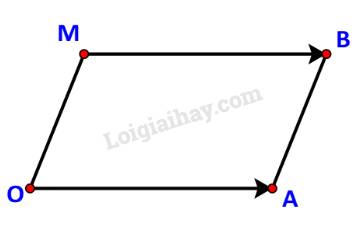
Do \(\overrightarrow {OA} = \left( {2;1} \right),\quad \overrightarrow {MB} = \left( {3 - x;3 - y} \right)\) nên
\(\overrightarrow {OA} = \overrightarrow {MB} \Leftrightarrow \left\{ \begin{array}{l}2 = 3 - x\\1 = 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\)
Vậy điểm cần tìm là M (1; 2).

A(m-1;-1); B(2;2-2m); C(m+3;3)
\(\overrightarrow{AB}=\left(2-m+1;2-2m+1\right)\)
=>\(\overrightarrow{AB}=\left(3-m;3-2m\right)\)
\(\overrightarrow{AC}=\left(m+3-m+1;3+1\right)\)
=>\(\overrightarrow{AC}=\left(4;4\right)\)
Để A,B,C thẳng hàng thì \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\)
=>3-m=3-2m
=>m=0
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(3-m;3-2m\right)\\\overrightarrow{AC}=\left(4;4\right)\end{matrix}\right.\)
3 điểm A;B;C thẳng hàng khi và chỉ khi \(\overrightarrow{AB}=k\overrightarrow{AC}\) với \(k\ne0\)
Hay \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\Rightarrow m=0\)

Lời giải:
Gọi $G(a,b)$ là trọng tâm tam giác. Ta có:
$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$
$\Leftrightarrow (1-a, 4-b)+(2-a, -3-b)+(1-a, -2-b)=(0,0)$
$\Leftrightarrow (1-a+2-a+1-a, 4-b-3-b-2-b)=(0,0)$
$\Leftrightarrow (5-3a, -1-3b)=(0,0)$
$\Rightarrow 5-3a=0; -1-3b=0$
$\Rightarrow a=\frac{5}{3}; b=\frac{-1}{3}$
b.
Để $A,B,D$ thẳng hàng thì:
$\overrightarrow{AB}=k\overrightarrow{AD}$ với $k$ là số thực $\neq 0$
$\Leftrightarrow (1,-7)=k(-2, 3m-1)$
$\Leftrightarrow \frac{1}{-2}=\frac{-7}{3m-1}$
$\Rightarrow m=5$

\(\overrightarrow{AB}\left(-3;2\right)\); \(\overrightarrow{AC}\left(1;m-2\right)\).
Ba điểm A, B, C thẳng hàng khi và chỉ khi:
\(\dfrac{1}{-3}=\dfrac{m-2}{2}\Leftrightarrow-3\left(m-2\right)=2\)\(\Leftrightarrow m=\dfrac{4}{3}\).

Có vô số điểm N để A,B,N thẳng hàng, cho nên để tìm ra 1 điểm N cụ thể thì cần thêm điều kiện nữa (ví dụ N thuộc Ox, Oy hoặc đường thẳng nào đó)

a: Ảnh của A là:
x=1+3=4 và y=2+1=3
b: (d') là ảnh của (d) qua phép tịnh tiến vecto a=(3;-2)
=>(d'): x+y+c=0
Lấy B(1;4) thuộc (d)
=>B'(4;2)
Thay x=4 và y=2 vào (d'), ta được:
c+4+2=0
=>c=-6
d: Theo đề,ta có:
2+x=-1 và 4+y=3
=>x=-3 và y=-1
=>vecto u=(-3;-1)
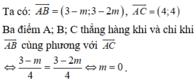
Đề sai rồi bạn