Tìm các số ngyên x,y biết:
(2x + 5y + 1)(2|x| + y + x2 +x) =105
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$3xy-2x+5y=9$
$x(3y-2)+5y=9$
$3x(3y-2)+15y=27$
$3x(3y-2)+5(3y-2)=17$
$(3x+5)(3y-2)=17$
Do $x,y$ nguyên nên $3x+5, 3y-2$ cũng là số nguyên. Ta có bảng sau: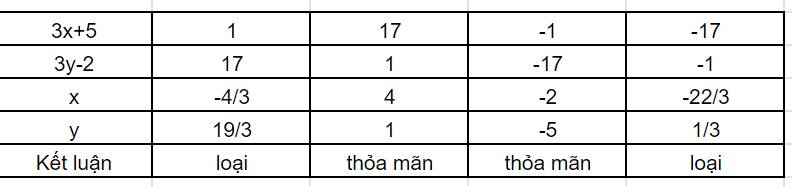

Do VP là số lẻ
<=> 2x + 5y + 1 là số lẻ và \(2^{\left|x\right|}+y+x^2+x\) là số lẻ
<=> y chẵn và \(2^{\left|x\right|}+y+x\left(x+1\right)\) là số lẻ
=> \(2^{\left|x\right|}\) là số lẻ (do y chẵn và x(x+1) chẵn)
=> x = 0
PT <=> \(\left(5y+1\right)\left(1+y\right)=105\)
<=> y = 4 (thử lại -> thỏa mãn)
KL: x = 0; y = 4


đậu xanh đậu đỏ
đậu đen đậu vàng
bạn ơi cùng đậu
xem vui không nào...



thi cấp tỉnh mà với có 1 số bài thi vào chuyên đại học với cấp 3 nữa
Bài 2: Ta có:
\(\left(2x+5y+1\right)\left(2020^{\left|x\right|}+y+x^2+x\right)=105\) là số lẻ
\(\Rightarrow\left\{{}\begin{matrix}2x+5y+1\\2020^{\left|x\right|}+y+x^2+x\end{matrix}\right.\) đều lẻ
\(\Rightarrow y⋮2\)\(\Rightarrow2020^{\left|x\right|}⋮̸2\Leftrightarrow\left|x\right|=0\Leftrightarrow x=0\).
Thay vào tìm được y...

qứadsxdfghjkla
tyuikol;pkjm