so sánh hơn dùng để so sánh 1ng vs nhiều ng hoặc 1 vật vs nhiầu vật đk ko ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 3 2022
Tham khảo:
Hạt trần | Hạt kín |
- Rễ, thân, lá thật. | - Rễ thân, lá thật; rất đa dạng. |
- Có mạch dẫn. | - Có mạch dẫn hoàn thiện. |
- Chưa có hoa, quả. Cơ quan sinh sản là nón. | - Có hoa: Cơ quan sinh sản là hoa quả. |
- Hạt nằm trên lá noãn hở. | - Hạt nằm trong quả. |
16 tháng 3 2022
Giống nhau
- Có rễ thân lá thực sự.
- Cấu tạo bên trong của dương xỉ đã có mạch dẫn làm chức năng vận chuyển.
Khác nhau
- Cơ quan sinh sản của dương sỉ là túi bào tử còn của cây hạt trần là các nón.
H
19 tháng 6 2023
Bài 1
Mình làm mẫu một số câu thôi nhé
\(9,\sqrt{5}=\left(\sqrt{5}\right)^2=5\\ \sqrt{6}=\left(\sqrt{6}\right)^2=6\)
Vì \(5< 6\)
\(\Rightarrow\sqrt{5}< \sqrt{6}\)
\(10,2\sqrt{5}=\left(2\sqrt{5}\right)^2=20\\ \sqrt{7}=\left(\sqrt{7}\right)^2=7\)
Vì \(20>7\)
\(\Rightarrow2\sqrt{5}>\sqrt{7}\)
\(11,5\sqrt{2}=\left(5\sqrt{2}\right)^2=50\\ 2\sqrt{3}=\left(2\sqrt{3}\right)^2=12\)
Vì \(50>12\Rightarrow5\sqrt{2}>2\sqrt{3}\)
\(12,2\sqrt{6}=\left(2\sqrt{6}\right)^2=24\\ 5=5^2=25\)
Vì \(25>24\Rightarrow5>2\sqrt{6}\)
\(13,\sqrt{7}=\left(\sqrt{7}\right)^2=7\\ 2=2^2=4\)
Vì \(7>4\Rightarrow\sqrt{7}>2\)
\(14,3=3^2=9\\ \sqrt{5}=\left(\sqrt{5}\right)^2=5\)
Vì \(9>5\Rightarrow3>\sqrt{5}\)
\(15,3\sqrt{6}=\left(3\sqrt{6}\right)^2=54\)
Vì \(54>1\Rightarrow3\sqrt{6}>1\)
\(16,2\sqrt{2}=\left(2\sqrt{2}\right)^2=8\\ 3=3^2=9\)
Vì \(8< 9\Rightarrow2\sqrt{2}< 3\)
Phương pháp làm dạng bài này là bình phương hai vế rồi so sánh
H
19 tháng 6 2023
Bài 2
Gợi ý : Biểu thức dưới dấu căn \(\ge\) 0
Lưu ý : Nếu biểu thức dưới dấu căn ở dưới mẫu thì \(>0\)
\(21,ĐK:4x^2-12x+9>0\\ \Rightarrow\left(2x-3\right)^2>0\\ \Leftrightarrow x\ne\dfrac{3}{2}\)
\(22,ĐK:x^2-8x+15\ge0\\ \Rightarrow\left[{}\begin{matrix}x\le3\\x\ge5\end{matrix}\right.\)
\(23,ĐK:\left\{{}\begin{matrix}x-2\ge0\\x-5\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge2\\x\ne5\end{matrix}\right.\)
\(24,ĐK:\left\{{}\begin{matrix}\dfrac{2+x}{5-x}\ge0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2+x\ge0\\5-x\ge0\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x\le5\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x< 5\end{matrix}\right.\left(t/m\right)\)
Hoặc
\(\left\{{}\begin{matrix}2+x\le0\\5-x\le0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\le-2\\x\ge5\\x\ne5\end{matrix}\right.\left(loại\right)\)
V
violet
Giáo viên
19 tháng 4 2016
- Vì dùng đòn bẩy sẽ giảm độ lớn của lực nên ta nâng vật lên dễ dàng hơn.
- Dùng đòn bẩy đưa vật lên sẽ nhẹ hơn khi dùng tay kéo vật lên, vì cánh tay đòn đến điểm tựa càng dài thì lực nâng càng nhỏ.
3 tháng 2 2021
Hai vật có cùng khối lượng ở độ cao khác nhau h1> h2. So sánh thế năng của hai vật?
A. Thế năng của hai vật bằng nhau.
B. Thế năng của vật 1 lớn hơn vật 2.
C. Thế năng của vật 2 lớn hơn vật 1.
D. Không đủ cơ sở để so sánh.
TH
1 tháng 4 2021
Chào Minh Anh Can nhé!
Cấu trúc so sánh hơn trong tiếng Anh
Cấu trúc với tính từ ngắn (Short Adj): thêm đuôi “er” vào sau tính từ hoặc phó từ ngắn.
S + V + adj/adv + er + than + N/pronoun
Lưu ý: Với tính từ có âm tận cùng là “y” thì phải đổi thành “i” thêm “er” và nó bị coi là tính từ ngắn. Ex: pretty => prettier
Trong trường hợp tính từ ngắn có 1 nguyên âm kẹp giữa 2 phụ âm tận cùng thì phải gấp đôi phụ âm cuối. Ex: big => bigger
Tính từ dài (Long Adj): thêm more/less.
S + V + more/less + adj/adv + than + N/pronoun
Ex: Lan is more beautiful than me.
Chúc em học vui vẻ và có nhiều trải nghiệm bổ ích tại Hoc24.vn nhé!
28 tháng 12 2020
gọi vật a là f1
vật b là f2
ta có vật 1 dao động nhanh hơn vì f1>f2 =>vật 1 phát ra âm cao hơn vật 2
DD
Đoàn Đức Hà
Giáo viên
2 tháng 7 2021
\(B=\frac{1}{2^2}+\frac{1}{4^2}+\frac{1}{6^2}+...+\frac{1}{\left(2n\right)^2}\)
\(2B=\frac{1}{2^2}+\frac{1}{2^2}+\frac{1}{4^2}+\frac{1}{4^2}+\frac{1}{6^2}+\frac{1}{6^2}+...+\frac{1}{\left(2n\right)^2}+\frac{1}{\left(2n\right)^2}\)
\(< \frac{1}{2^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+\frac{1}{6^2}+...+\frac{1}{\left(2n-1\right)^2}+\frac{1}{\left(2n\right)^2}\)
\(< \frac{1}{2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+\frac{1}{5.6}+...+\frac{1}{\left(2n-2\right)\left(2n-1\right)}+\frac{1}{\left(2n-1\right)2n}\)
\(=\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+...+\frac{1}{2n-1}-\frac{1}{2n}\)
\(=1-\frac{1}{2n}< 1\)
Suy ra \(B< \frac{1}{2}\).
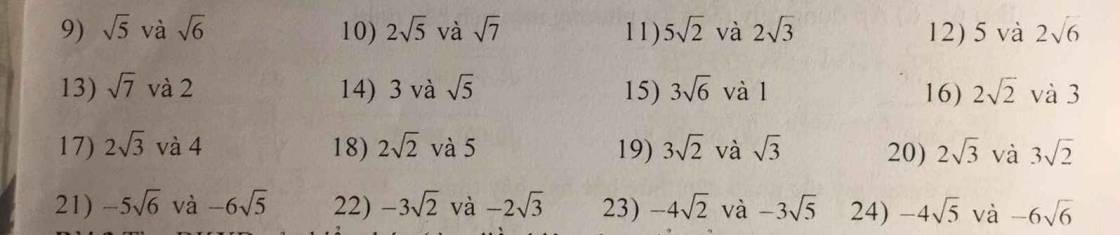
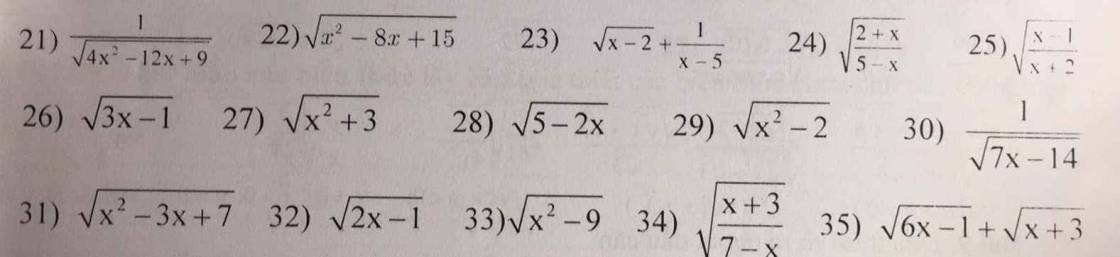
đúng
đúng nha bro