Câu 32: Tam giác đều có số trục đối xứng là
A. 3. B.1. C.2. D.0.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NK
4
Những câu hỏi liên quan
2 tháng 12 2023
Các phát biểu về đối xứng hình học như sau:
A. Hình tròn: Hình tròn có vô số trục đối xứng và 1 tâm đối xứng. Điều này đúng.
B. Hình vuông: Hình vuông có 4 trục đối xứng, tương ứng với 4 đường đối xứng qua các đỉnh của hình vuông. Điều này cũng đúng.
C. Hình tam giác đều: Hình tam giác đều có 3 trục đối xứng và 1 tâm đối xứng. Điều này cũng đúng.
D. Hình lục giác đều: Hình lục giác đều có 1 tâm đối xứng và 6 trục đối xứng, tương ứng với 6 đường đối xứng qua các đỉnh của hình lục giác đều. Điều này cũng đúng.
Vậy tất cả các phát biểu đều đúng. 😊
CM
3 tháng 10 2019
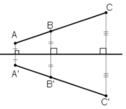
b) Đúng vì hai tam giác đối xứng nhau qua một trục thì bằng nhau nên chúng cũng có chu vi bằng nhau.
c) Đúng. Tất cả các đường thẳng đi qua tâm đều là trục đối xứng của đường tròn.
d) Sai.
Mọi đoạn thẳng AB đều có hai trục đối xứng là đường thẳng AB và đường trung trực của đoạn thẳng AB.
VN
Võ Ngọc Phương
VIP
28 tháng 12 2023
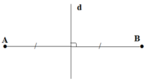
Ta có:
Hình chữ nhật có 2 trục đối xứng.
Hình thang cân có 1 trục đối xứng.
Hình bình hành không có trục đối xứng.
Hình thoi có 2 trục đối xứng.
Hình tam giác đều có 3 trục đối xứng.
Hình vuông có 4 trục đối xứng.
\(\Rightarrow\) Chọn đáp án C.
\(#Nulc`\)
a
Câu 32: Tam giác đều có số trục đối xứng là
A. 3. B.1. C.2. D.0.