Lúc 7 giờ sáng một ô tô đi từ A đến B. Lúc 7 giờ 30 phút, một xe máy đi từ B về A với vận tốc kém vận tốc ô tô là 24 km/h. Ô tô đến B được 1 giờ 20 phút thì xe máy mới đến A. TÍnh vận tốc mỗi xe biết quãng đường AB dài 120 kkm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 6 2018
Gọi vận tốc của xe máy là x (km/h; x > 0)
Vận tốc của ô tô là x + 24 (km/h)
Thời gian xe máy đi hết quãng đường là: 120/x (h)
Thời gian ô tô đi hết quãng đường là: 120/(x+4) (h)
Đổi 30 phút = 1/2 (h), 20 phút = 1/3 (h)
Theo đề bài ta có phương trình:
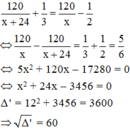
Phương trình có hai nghiệm x 1 = − 12 – 60 = −72 (loại) và x 2 = −12 + 60 = 48 (tmđk)
Vậy vận tốc xe máy là 48 km/h và vận tốc ô tô là 48 + 24 = 72 km/h
Đáp án: D
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
Gọi vận tốc xe máy là x(km/h) với x>0
Vận tốc ô tô là: \(x+24\) (km/h)
Thời gian xe máy đi hết quãng đường AB là: \(\dfrac{120}{x}\) giờ
Thời gian ô tô đi hết quãng đường là: \(\dfrac{120}{x+24}\) giờ
Do xe máy xuất phát sau ô tô \(\dfrac{1}{2}\) giờ nhưng ô tô đến trước xe máy 1h20ph=\(\dfrac{4}{3}\) giờ nên thời gian ô tô đi ít hơn thời gian xe máy đi là \(\dfrac{4}{3}-\dfrac{1}{2}=\dfrac{5}{6}\) giờ
Ta có phương trình:
\(\dfrac{120}{x}-\dfrac{120}{x+24}=\dfrac{5}{6}\)
\(\Rightarrow720\left(x+24\right)-720x=5x\left(x+24\right)\)
\(\Leftrightarrow x^2+24x-576=0\) \(\Rightarrow\left[{}\begin{matrix}x=48\\x=-72\left(loại\right)\end{matrix}\right.\)
Vậy vận tốc xe máy là 48 (km/h) và vận tốc ô tô là 72 (km/h)
NN
25 tháng 3 2020
Gọi vận tốc ô tô là: x ( km/h ) ( x > 24 )
=) vận tốc xe máy là: x - 24 ( km/h )
Thời gian để ô tô đi hết quãng đường AB là: \(\frac{120}{x}\)( giờ )
Thời gian đẻ xe máy đi hết quãng đường AB là: \(\frac{120}{x-24}\)( giờ )
VÌ ô tô đến B được \(\frac{4}{3}\)giờ thì xe máy mới đén A cũng như ô tô đi trươc xe máy \(\frac{1}{2}\)giờ nên ta có phương trình:
\(\frac{120}{x-24}-\frac{4}{3}=\frac{120}{x}-\frac{1}{2}\)
\(\frac{120}{x-24}-\frac{120}{x}=\frac{5}{6}\)
\(\frac{720x}{6x.\left(x-24\right)}-\frac{720.\left(x-24\right)}{6x.\left(x-24\right)}=\frac{5x.\left(x-24\right)}{6x.\left(x-24\right)}\)
\(720x-720+17280=5x^2-120x\)
\(5x^2-120x-17280=0\)
\(x^2-24x-3456=0\)
\(\left(x-72\right).\left(x+48\right)=0\)
\(\orbr{\begin{cases}x=72\\x=-48\left(lo\text{ại}\right)\end{cases}}\)
Vận tốc ô tô là: 72 km/h
Vận tốc xe máy là: 48 km/h
26 tháng 3 2020
Gọi vận tốc xe máy là x (km/h) (x>0)
thì vận tốc ô tô là: x + 24 (km/h)
Thời gian xe máy đi quãng đường AB là: \(\frac{120}{x}\)(h)
Thời gian ô tô đi quãng đường AB là:\(\frac{120}{x+24}\)(h)
Thời gian xe máy đi nhiều hơn ô tô: 1h20' - (7h30' - 7h) = 50' = \(\frac{5}{6}\) (h)
Ta có phương trình: \(\frac{120}{x}-\frac{120}{x+24}=\frac{5}{6}\)
<=> 6.[120(x+24) - 120x] = 5x(x+24)
<=> 720(x+24) - 720x = 5x^2 + 120x
<=> 5x^2 + 120x - 17280 = 0
<=> x = 48 (TMĐK) hoặc x = -72 (không TMĐK)
Vậy vận tốc xe máy là 48 km/h
vận tốc ô tô là: 48+24=72 (km/h)
AH
Akai Haruma
Giáo viên
28 tháng 5 2022
Lời giải:
Đổi 20' = 1/3 giờ
Thời gian ô tô đi: $AB:42$ (giờ)
Thời gian xe máy đi: $AB:36$ (giờ)
Vì xe máy đi lâu hơn ô tô 20 phút nên:
$AB:36-AB:42=\frac{1}{3}$
$AB\times \frac{1}{36}-AB\times \frac{1}{42}=\frac{1}{3}$
$AB\times (\frac{1}{36}-\frac{1}{42})=\frac{1}{3}$
$AB\times \frac{1}{252}=\frac{1}{3}$
$AB=\frac{1}{3}\times 252=84$ (km)
Thời gian ô tô đi đến B: $84:42=2$ (giờ)
Ô tô đi đến B lúc:
$7h30'+2h=9h30'$
DD
Đoàn Đức Hà
Giáo viên
23 tháng 5 2022
Mỗi ki-lô-mét ô tô đi hết số giờ là:
\(1\div42=\dfrac{1}{42}\left(h\right)\)
Mỗi ki-lô-mét xe máy đi hết số giờ là:
\(1\div36=\dfrac{1}{36}\left(h\right)\)
Mỗi ki-lô-mét xe máy đi nhiều hơn ô tô số giờ là:
\(\dfrac{1}{36}-\dfrac{1}{42}=\dfrac{1}{252}\left(h\right)\)
Đổi: \(20'=\dfrac{1}{3}h\)
Quãng đường AB là:
\(\dfrac{1}{3}\div\dfrac{1}{252}=84\left(km\right)\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
23 tháng 5 2022
Trên cùng quãng đường vận tốc mỗi xe tỷ lệ nghịch với thời gian mỗi xe khi đi hết cùng một quãng đường
Vận tốc xe máy / vận tốc ô tô = thời gian ô tô / thời gian xe máy = 36/42 = 6/7
Chia thời gian ô tô đi hết quãng đường AB thành 6 phần bằng nhau thì thời gian xe máy đi hết quãng đường AB là 7 phần
20 phút = 1/3 giờ
Hiệu số phần bằng nhau là
7-6=1 phần
Giá trị 1 phần là
\(\dfrac{1}{3}:1=\dfrac{1}{3}\) giờ
Thời gian ô tô đi hết quãng đường AB là
\(6x\dfrac{1}{3}=2\) giờ
Thời gian ô tô đến B là
7 giờ 30 phút + 2 giờ = 9 giờ 30 phút
Quãng đường AB là
42x2=84 km