Cho ΔABC nhọn, nội tiếp đường tròn tâm (O). Gọi M là trung điểm của đường thẳng AC và K là chân đường vuông góc kẻ từ M xuống AB. Biết AB = 12cm, AC = 10cm và MK = 4cm
a) Tính độ dài đoạn thẳng AK
b) Gọi H là trung điểm của đoạn thẳng AB. Chứng minh CH vuông góc với AB
c) Tính bán kính đường tròn tâm O, tiếp xúc với đường thẳng BC
=============================================
Mọi người giúp mình bài này với, mình đang cần gấp lắm ạ!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\angle MFC=\angle MEC=90\Rightarrow MFEC\) nội tiếp
b) Ta có: \(\angle MFE=180-\angle MCE=\angle MAB\)
\(\angle FME=\angle FCE=\angle AMB\)
Xét \(\Delta AMB\) và \(\Delta MFE\):Ta có: \(\left\{{}\begin{matrix}\angle MFE=\angle MAB\\\angle FME=\angle AMB\end{matrix}\right.\)
\(\Rightarrow\Delta AMB\sim\Delta MFE\left(g-g\right)\Rightarrow\dfrac{BM}{BA}=\dfrac{ME}{FE}\Rightarrow BM.FE=ME.BA\)
c) Ta có: \(\Rightarrow\Delta AMB\sim\Delta MFE\Rightarrow\dfrac{MF}{FE}=\dfrac{MA}{AB}\Rightarrow2\dfrac{MF}{FE}=2\dfrac{MA}{AB}\)
\(\Leftrightarrow\dfrac{MF}{FQ}=\dfrac{MA}{AB}\)
Xét \(\Delta AMP\) và \(\Delta FMQ\):Ta có: \(\left\{{}\begin{matrix}\angle MFQ=\angle MAP\\\dfrac{MF}{FQ}=\dfrac{MA}{MB}\end{matrix}\right.\)
\(\Rightarrow\Delta AMP\sim\Delta FMQ\left(c-g-c\right)\)
d) Kẻ \(MD\bot AB\left(D\in AB\right)\)
Ta có: \(\angle MDA+\angle MFA=90+90=180\Rightarrow\) MDAF nội tiếp
\(\Rightarrow\angle DFA=\angle DMA=90-\angle DAM\)
Tương tự \(\Rightarrow\angle EFC=\angle EMC=90-\angle MCB\)
mà \(\angle DAM=\angle MCB\) (AMCB nội tiếp)\(\Rightarrow\angle DFA=\angle EFC\)
mà A,F,C thẳng hàng \(\Rightarrow\) \(\)D,F,E thẳng hàng
Ta có: \(\angle MQF=\angle MPA\left(\Delta MFQ\sim\Delta MAP\right)\Rightarrow\angle MQD=\angle MPD\)
\(\Rightarrow\) MDPQ nội tiếp mà \(\angle MDP=90\Rightarrow\angle PQM=90\)

Chọn đáp án D

* Chứng minh các tứ giác ABHF và BMFO nội tiếp.
- Từ giả thiết suy ra: 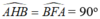
=> H và F thuộc đường tròn đường kính AB (quỹ tích cung chứa góc)
Vậy tứ giác ABHF nội tiếp đường tròn đường kính AB
- Gọi M là trung điểm của BC (gt), suy ra: OM ⊥ BC
Khi đó: 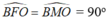
Nên M, F thuộc đường tròn đường kính OB(quỹ tích cung chứa góc).
Vậy tứ giác BMOF nội tiếp đường tròn đường kính OB
* Chứng minh HE // BD.
Dễ chứng minh tứ giác ACEH nội tiếp đường tròn đường kính AC.
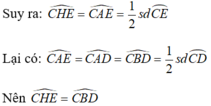
Và chúng ở vị trí so le trong suy ra: HE // BD


alo mấy bạn giúp tớ với