cho tứ giác ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, AC, CD, BD.
a) Tứ giác EFGH là hình gì?
b) các cạch AD và BC có điều kiện gì thì EFGH là hình chữ nhật? hình thoi? hình vuông?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 9 2019
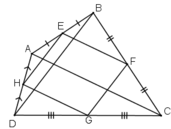
Ta có: EB = EA, FB = FC (gt)
⇒ EF là đường trung bình của ΔABC
⇒ EF // AC và EF = AC/2.
HA = HD, HC = GD
⇒ HG là đường trung bình của ΔADC
⇒ HG // AC và HG = AC/2.
Do đó EF // HG, EF = HG
⇒ EFGH là hình bình hành.
a) Hình bình hành EFGH là hình chữ nhật ⇔ EH ⊥ EF
⇔ AC ⊥ BD (vì EH // BD, EF// AC)
b) Hình bình hành EFGH là hình thoi
⇔ EF = EH
⇔ AC = BD (Vì EF = AC/2, EH = BD/2)
c) EFGH là hình vuông
⇔ EFGH là hình thoi và EFGH là hình chữ nhật
⇔ AC = BD và AC ⊥ DB.
21 tháng 4 2017
Ta có : HE, GF lần lượt là đường trung bình của tam giác ADB và tam giác CDB
=> HE // BD, GF // BD và BD = 2HE = 2GF
Tương tự : HG, EF lần lượt là đường trung bình của tam giác DAC và tam giác BAC
=> HG // AC, EF // AC và AC = 2HG = 2EF
Nên EFGH là hình bình hành.
a) Đề hình bình hành EFGH là hình chữ nhật thì EH ⊥ EF => BD ⊥ AC
Điều kiện phải tìm : Hai đường chéo AC, BD vuông góc với nhau.
b) Để hình bình hành EFGH là hình thoi thì EH = EF => BD = AC
Điều kiện phải tìm : Hai đường chéo AC và BD bằng nhau.
c) Để hình bình hành EFGH là hình vuông thì EFGH phải vừa là hình chữ nhật, vừa là hình thoi => BD ⊥ AC và BD = AC.
Điều kiện phải tìm : Hai đường chéo AC, BD vuông góc với nhau và bằng nhau.