Cho tam giác ABC nhọn có AB < AC . Trên cạnh BC lấy điểm E sao cho
AB= AE, gọi H là trung điểm của BE.
1.
Chứng minh tam giác ABH=tam giác AEH.
2.
Chứng minh AH vuông góc BE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 12 2023
1: Xét ΔABH và ΔAEH có
AB=AE
BH=EH
AH chung
Do đó: ΔAHB=ΔAHE
2: ΔAHB=ΔAHE
=>\(\widehat{AHB}=\widehat{AHE}\)
mà \(\widehat{AHB}+\widehat{AHE}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHE}=\dfrac{180^0}{2}=90^0\)
=>AH\(\perp\)BE
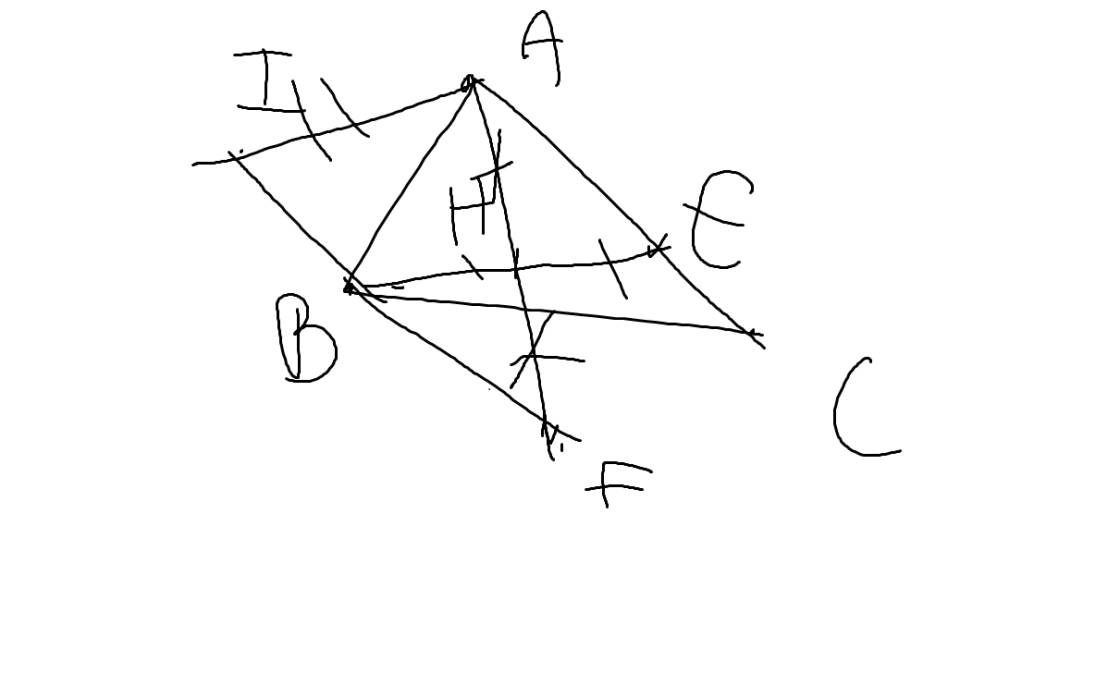
3: Sửa đề: Kẻ tia Ax//BE, trên Ax lấy I sao cho AI=BE(I và B nằm cùng phía so với AH)
a: Xét tứ giác ABFE có
H là trung điểm chung của AF và BE
=>ABFE là hình bình hành
=>BF=AE và BF//AE
b:
Xét tứ giác AEBI có
AI//BE
AI=BE
Do đó: AEBI là hình bình hành
=>BI//AE
Ta có: BF//AE
BI//AE
BI,BF có điểm chung là B
Do đó: F,B,I thẳng hàng
12 tháng 1 2022
1: Xét ΔABH và ΔAEH có
AB=AE
BH=EH
AH chung
Do đó: ΔABH=ΔAEH
2: Ta có: ΔABE cân tại A
mà AH là đường trung tuyến
nên AH là đường cao
3:
a: Xét tứ giác ABFE có
H là trung điểm BE
H là trung điểm của AF
Do đó: ABFE là hình bình hành
Suy ra; BF=AE
30 tháng 12 2021
1: Xét ΔABH và ΔAEH có
AB=AE
AH chung
BH=EH
Do đó: ΔABH=ΔAEH
5 tháng 1 2022
a: Xét ΔABH và ΔAEH có
AB=AE
\(\widehat{BAH}=\widehat{EAH}\)
AH chung
Do đó: ΔABH=ΔAEH
b: Ta có: ΔABH=ΔAEH
nên HB=HE
29 tháng 8 2023
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
BA=BH
Do đó; ΔBAE=ΔBHE
b: ΔBAE=ΔBHE
=>EA=EH
=>ΔEAH cân tại E
c: BA=BH
EA=EH
=>BE là trung trực của AH
d: Xét ΔBKC có
KH,CA là đường cao
KH cắt CA tại E
Do đó: E là trực tâm
=>BE vuông góc KC
2 tháng 7 2021
a) Xét ΔABC có AB=AC(gt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
Suy ra: \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy)
hay \(\widehat{ABH}=\widehat{ACH}\)
b) Xét ΔABH và ΔACH có
AB=AC(ΔABC cân tại A)
AH chung
BH=CH(H là trung điểm của BC)
Do đó: ΔABH=ΔACH(c-c-c)
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)(hai góc tương ứng)
hay \(\widehat{MAE}=\widehat{NAE}\)
Xét ΔAME và ΔANE có
AM=AN(gt)
\(\widehat{MAE}=\widehat{NAE}\)(cmt)
AE chung
Do đó: ΔAME=ΔANE(c-g-c)
c) Ta có: ΔAME=ΔANE(cmt)
nên \(\widehat{AEM}=\widehat{AEN}\)(hai góc tương ứng)
mà \(\widehat{AEM}+\widehat{AEN}=180^0\)(hai góc so le trong)
nên \(\widehat{AEM}=\widehat{AEN}=\dfrac{180^0}{2}=90^0\)
Suy ra: AH⊥MN tại E(1)
Ta có: ΔABH=ΔACH(cmt)
nên \(\widehat{AHB}=\widehat{AHC}\)(hai góc tương ứng)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
Suy ra: AH⊥BC tại H(2)
Từ (1) và (2) suy ra MN//BC(Đpcm)
