trên đường thẳng d lấy 3 điểm A;B;C cố đinh theo thứ tự đó .vẽ đường tròn O bất kì qua BC (BC ko phải đường kính đường tròn tâm O) .kẻ 2 tiếp tuyến AE;AF đến đường tròn O .gọi I là trung điểm của BC.K là trung điểm của EF. giao điểm của FI với đường tròn O là D.chứng minh
a) AE^2=AB.AC
b) năm điểm A;E;O;I;F cùng thuộc 1 đường tròn
c) ED//AC
d) khi đường tròn O thay đổi thì tâm đường tròn ngoại tiếp tam giác OIK luôn thuộc 1 đường thẳng cố định


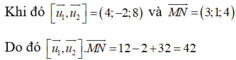
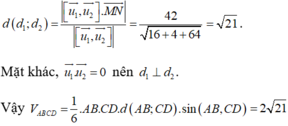
2 tam giác HIE và HFA đồng dạng do có góc tại đỉnh H bằng nhau và góc HIE = góc FA (cùng chắn cung A của Q) => HI / HF = HE / HA => HI*HA = HE*HF ♦
2 ∆ HEB và HCF đồng dạng do có góc tại đỉnh H bằng nhau và góc HEB = góc HCF (cùng chắn cung BF của O) => HE / HC = HB / HF => HB*HC = HE*HF ♥
(Nếu bạn đã học phương tích của điểm đối với đường tròn thì có ngay ♦ và ♥ không cần cm vì ♦ chính là pt của H đối với Q còn ♥ là pt của H đối với O)
♦, ♥ => HI*HA = HB*HC => HI*(AI - HI) = (x - HI)(x + HI) => HI*AI = x²
=> HI = x² / AI = hằng số (A, I cố định nên AI không đổi)
=> H cố định.
Dễ thấy OIHK nội tiếp đường tròn (P) => đường tròn ngoại tiếp ∆ IOK chính là (P). Tâm đường tròn (P) dĩ nhiên nằm trên trung trực k của HI mà trung trực này cố định do H, I cố định. Vậy tâm đường tròn ngoại tiếp tam giác OIK luôn thuộc k cố định
có người làm rồi kìa