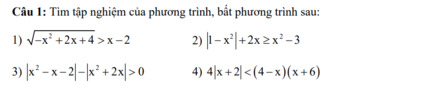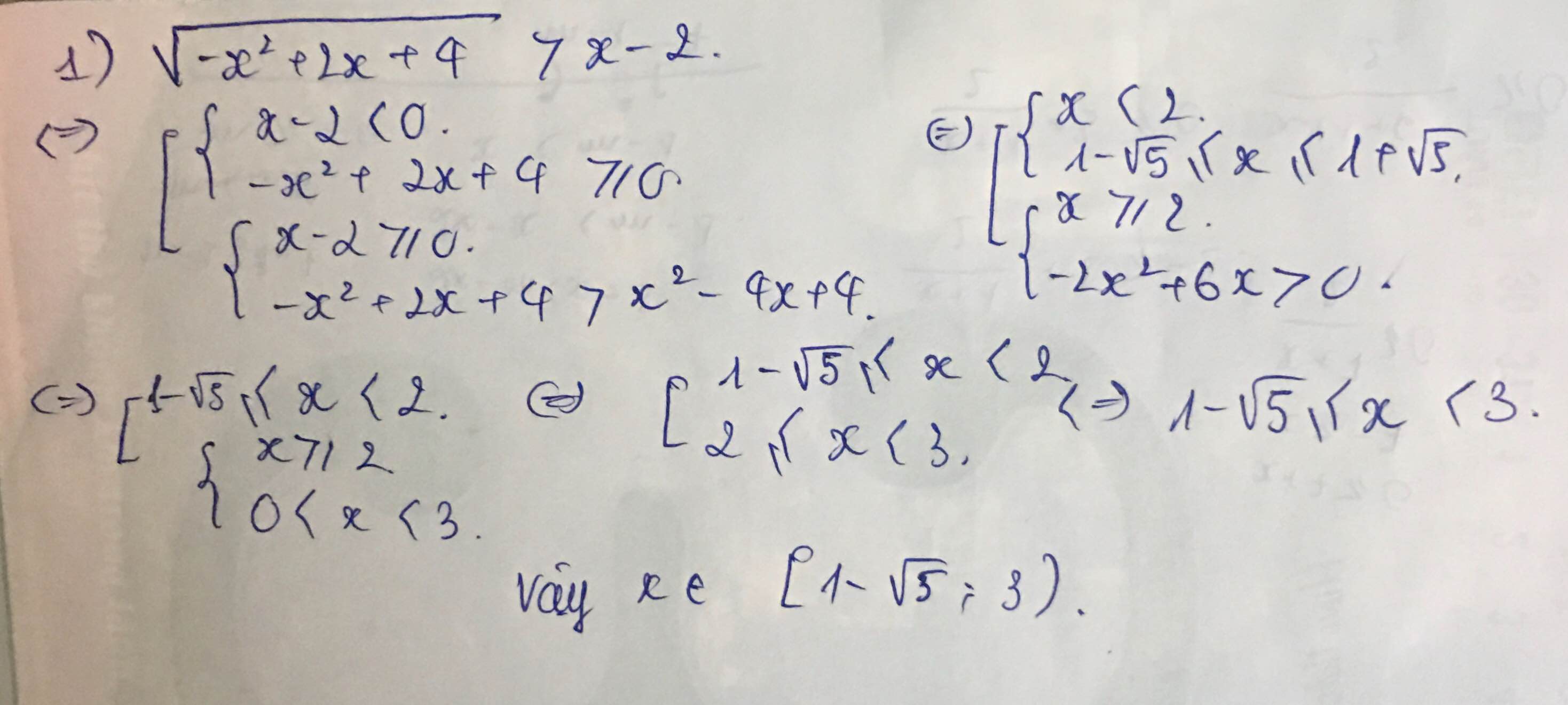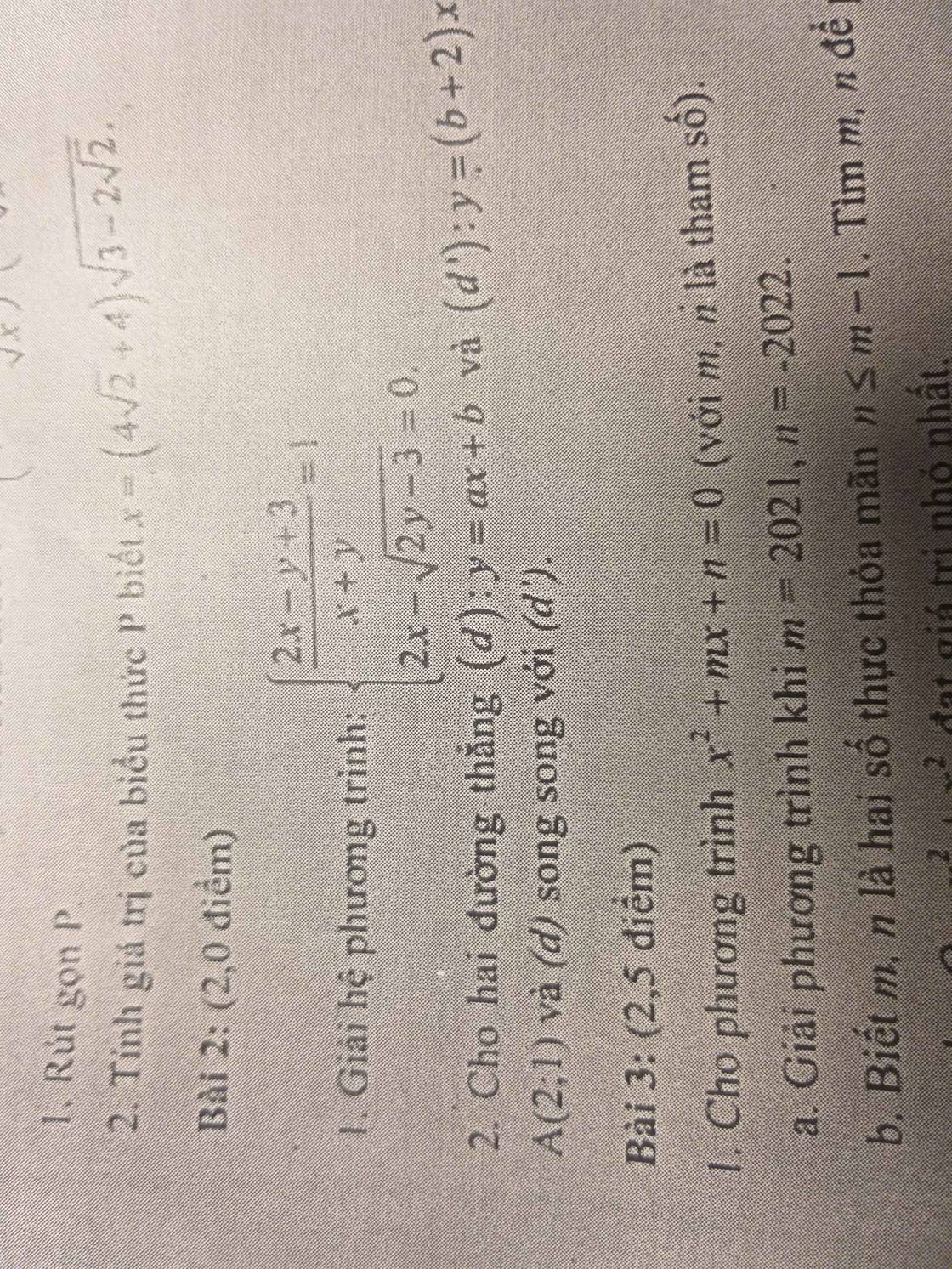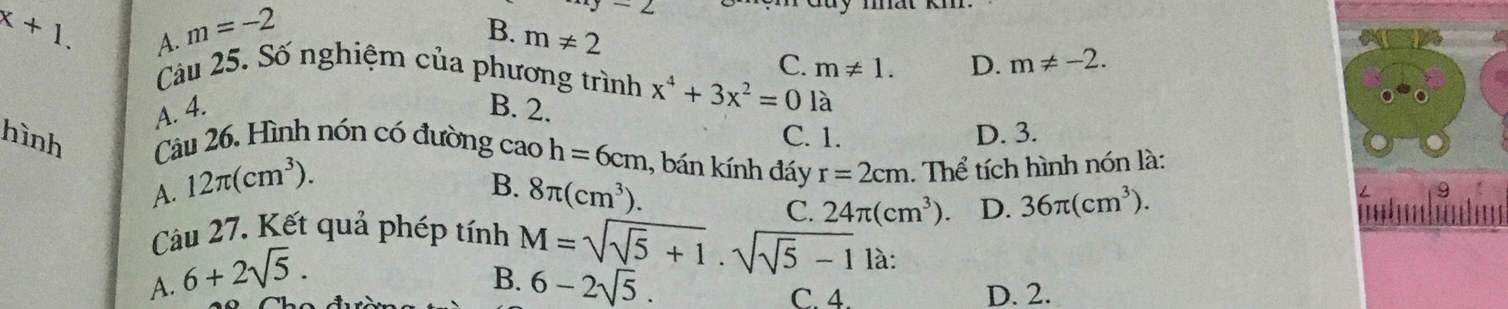Giải giúp mk câu 4 với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Diện tích lớn nhất mà vật đó tiếp xúc với mặt bàn :
\(40.20=800\left(cm^2\right)=0,08\left(m^2\right)\)
Diện tích nhỏ nhất mà vật đó tiếp xúc với mặt bàn :
\(20.20=400\left(cm^2\right)=0,04\left(m^2\right)\)
Áp suất lớn nhất mà vật tác dụng lên mặt bàn :
\(P=\dfrac{F}{S}=\dfrac{3000}{0,04}=75000\left(Pa\right)\)
Áp suất nhỏ nhất mà vật tác dụng lên mặt bàn :
\(P=\dfrac{F}{S}=\dfrac{3000}{0,08}=37500\left(Pa\right)\)

\(5;;\sqrt{\left(x+5\right)\left(3x+4\right)}>4\left(x-1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}4\left(x-1\right)\le0\\\left(x+5\right)\left(3x+4\right)\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}4\left(x-1\right)\ge0\\\left(x+5\right)\left(3x+4\right)\ge0\\\left(x+5\right)\left(3x+4\right)>16\left(x-1\right)^2\end{matrix}\right.\end{matrix}\right.\)
\(TH:\left\{{}\begin{matrix}4\left(x-1\right)\le0\\\left(x+5\right)\left(3x+4\right)\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le1\\\left[{}\begin{matrix}x\le-5\\x\ge-\dfrac{4}{3}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x\in(-\infty;-5]\cup\left[-\dfrac{4}{3};1\right]\left(1\right)\)
\(TH:\left\{{}\begin{matrix}4\left(x-1\right)\ge0\\\left(x+5\right)\left(3x+4\right)\ge0\\\left(x+5\right)\left(3x+4\right)>16\left(x-1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\\left[{}\begin{matrix}x\le-5\\x\ge-\dfrac{4}{3}\end{matrix}\right.\\-\dfrac{1}{13}< x< 4\\\end{matrix}\right.\)\(\Rightarrow x\in[1;4)\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow x\in(-\infty;5]\cup[\dfrac{-4}{3};4)\)
\(6;;;;\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{49x^2+7x-42}< 181-14x\)
(đoạn 49x^2+7x+42 chắc bạn viết sai đề dấu"-" thành "+")
\(đk:\left\{{}\begin{matrix}7x+7\ge0\\7x-6\ge0\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{6}{7}\)
\(bpt\Leftrightarrow\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{\left(7x+7\right)\left(7x-6\right)}+14x+1< 182\left(1\right)\)
\(đặt:\sqrt{7x+7}+\sqrt{7x-6}=t>0\)
\(\Rightarrow t^2=14x+1+2\sqrt{\left(7x+7\right)\left(7x-6\right)}\)
\(\Rightarrow\left(1\right)\Leftrightarrow t^2+t< 182\Leftrightarrow-14< t< 13\)
\(\Rightarrow\sqrt{7x+7}+\sqrt{7x-6}< 13\Leftrightarrow14x+1+2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 169\)
\(\Leftrightarrow2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 168-14x\)
\(\Leftrightarrow\left\{{}\begin{matrix}168-14x\ge0\\\left(7x+7\right)\left(7x-6\right)\ge0\\4\left(7x+7\right)\left(7x-6\right)< \left(168-14x\right)^2\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le12\\\left[{}\begin{matrix}x\le-1\\x\ge\dfrac{6}{7}\end{matrix}\right.\\x< 6\\\end{matrix}\right.\)\(\Rightarrow\dfrac{6}{7}\le x< 6\)

Câu 4:
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
a) Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{DA}{DC}=\dfrac{BA}{BC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{DA}{DC}=\dfrac{6}{10}=\dfrac{3}{5}\)

ĐK: \(\left\{{}\begin{matrix}x\ne-y\\y\ge\dfrac{3}{2}\end{matrix}\right.\).
\(\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}=1\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}-1=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}-\dfrac{x+y}{x+y}=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y+3-x-y=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2y+3=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-\left(2y-3\right)=0\\2x-\sqrt{2y-3}=0\end{matrix}\right..\)
Đặt a = x, b = \(\sqrt{2y-3}\).
Hệ phương trình trở thành: \(\left\{{}\begin{matrix}a-b^2=0\\2a-b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\2b^2-b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\b\left(2b-1\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\\left[{}\begin{matrix}b=0\\b=\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\left\{{}\begin{matrix}\left[{}\begin{matrix}a=0\\a=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}b=0\\b=\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\2y-3=\dfrac{1}{4}\end{matrix}\right.\end{matrix}\right.\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\2y=\dfrac{13}{4}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\y=\dfrac{13}{8}\end{matrix}\right.\end{matrix}\right..\)
Vậy hệ phương trình có nghiệm (x;y) \(\in\) \(\left\{\left(0;\dfrac{3}{2}\right),\left(\dfrac{1}{4};\dfrac{13}{8}\right)\right\}\).

\(I=\int\dfrac{2}{2+5sinxcosx}dx=\int\dfrac{2sec^2x}{2sec^2x+5tanx}dx\\ =\int\dfrac{2sec^2x}{2tan^2x+5tanx+2}dx\)
We substitute :
\(u=tanx,du=sec^2xdx\\ I=\int\dfrac{2}{2u^2+5u+2}du\\ =\int\dfrac{2}{2\left(u+\dfrac{5}{4}\right)^2-\dfrac{9}{8}}du\\ =\int\dfrac{1}{\left(u+\dfrac{5}{4}\right)^2-\dfrac{9}{16}}du\\ \)
Then,
\(t=u+\dfrac{5}{4}\\I=\int\dfrac{1}{t^2-\dfrac{9}{16}}dt\\ =\int\dfrac{\dfrac{2}{3}}{t-\dfrac{3}{4}}-\dfrac{\dfrac{2}{3}}{t+\dfrac{3}{4}}dt\)
Finally,
\(I=\dfrac{2}{3}ln\left(\left|\dfrac{t-\dfrac{3}{4}}{t+\dfrac{3}{4}}\right|\right)+C=\dfrac{2}{3}ln\left(\left|\dfrac{tanx+\dfrac{1}{2}}{tanx+2}\right|\right)+C\)

\(x^4+3x^2=0\)
Có \(x^4\ge0;\forall x\); \(3x^2\ge0;\forall x\)
=> VT\(\ge0;\forall x\)
Dấu = xảy ra <=> x=0
Ý C