Cho lục giác lồi ABCDEF có các cặp cạnh đối song song với nhau. Chứng minh rằng SACE >= 1/2 SABCDEF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cần chứng minh
\(\overrightarrow{A_1B_1}=\overrightarrow{E_1D_1}\), \(_{ }\overrightarrow{B_1C_1}=\overrightarrow{F_1E_1}\), \(\overrightarrow{C_1D_1}=\overrightarrow{A_1F_1}\)
Ta có :
\(\overrightarrow{OA_1}=\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}}{3}\) ; \(\overrightarrow{OD_1}=\frac{\overrightarrow{OD}+\overrightarrow{OE}+\overrightarrow{OF}}{3}\)
\(\overrightarrow{OB_1}=\frac{\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}}{3}\) ; \(\overrightarrow{OE_1}=\frac{\overrightarrow{OE}+\overrightarrow{OF}+\overrightarrow{OA}}{3}\)
Từ đó suy ra :
\(\overrightarrow{A_1B_1}+\overrightarrow{OD_1}=\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{OE}+\overrightarrow{OF}}{3}=\overrightarrow{0B_1}+\overrightarrow{OE_1}\)
và do đó
\(\overrightarrow{A_1B_1}=\overrightarrow{E_1D_1}\)
Tương tự ta cũng có \(\overrightarrow{B_1C_1}=\overrightarrow{F_1E_1}\) ,\(\overrightarrow{C_1D_1}=\overrightarrow{A_1F_1}\) => Điều phải chứng minh


gọi giao điểm của AD và EB là O mà ABDE là hình bình hành nên O là trung điểm EB
Nối BF ; CE ta đc BCEF là hình bình hành nên EB và CF cắt nhau tại trung điểm EB là O

Ta có:
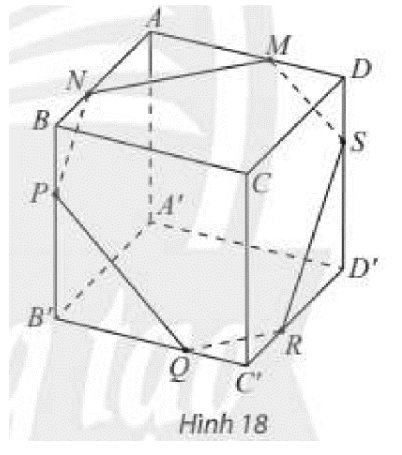
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( \alpha \right) \cap \left( {ABC{\rm{D}}} \right) = MN\\\left( \alpha \right) \cap \left( {A'B'C'D'} \right) = Q{\rm{R}}\end{array} \right\} \Rightarrow MN\parallel Q{\rm{R}}\)
\(\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( \alpha \right) \cap \left( {AA'B'B} \right) = NP\\\left( \alpha \right) \cap \left( {CC'D'D} \right) = R{\rm{S}}\end{array} \right\} \Rightarrow NP\parallel R{\rm{S}}\)
\(\left. \begin{array}{l}\left( {AA'D'D} \right)\parallel \left( {BB'C'C} \right)\\\left( \alpha \right) \cap \left( {AA'D'D} \right) = M{\rm{S}}\\\left( \alpha \right) \cap \left( {BB'C'C} \right) = PQ\end{array} \right\} \Rightarrow M{\rm{S}}\parallel PQ\)