Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a, H là trung điểm AB, (SH) ⊥ (ABC). Góc đường thẳng SB và mặt phẳng (SAC) bằng 45o. Tính SH?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Lời giải.
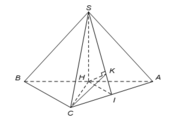
Ta có
![]()
![]()
![]()
Từ (1) và (2)
![]()
Gọi I là trung điểm AC
![]()
Mặt khác
![]()
Từ (3) và (4)
![]()
![]()
![]()
![]()
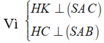
nên góc giữa hai mặt phẳng (SAC) và (SAB) bằng góc giữa hai đường thẳng HK và HC.
Xét tam giác CHK vuông tại K, có
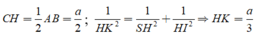
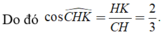

Đáp án A
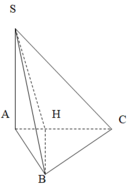
Kẻ B H ⊥ A C ⇒ B H ⊥ ( S A C )
Suy ra SH là hình chiếu vuông góc của SB lên (SAC)
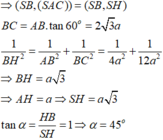

Đáp án A
Kẻ B H ⊥ A C ⇒ B H ⊥ S A C
Suy ra SH là hình chiếu vuông góc của SB lên (SAC)
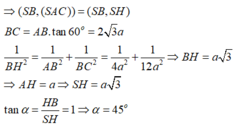
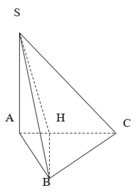
Trong mp (SAB), qua B dựng đường thẳng song song SH, cắt tia AS kéo dài tại D
\(\Rightarrow\) SH là đường trung bình tam giác ABD \(\Rightarrow BD=2SH\) và \(BD\perp\left(ABC\right)\)
Gọi M là trung điểm AC \(\Rightarrow BM\perp AC\Rightarrow AC\perp\left(BDM\right)\)
Trong mp (BDM), kẻ \(BK\perp DM\Rightarrow BK\perp\left(SAC\right)\Rightarrow\widehat{BSK}\) là góc giữa SB và (SAC)
\(\Rightarrow\widehat{BSK}=45^0\Rightarrow SB=BK\sqrt{2}\)
\(\Rightarrow AD=2SA=2SB=2\sqrt{2}BK\Rightarrow BD^2=AD^2-AB^2=8BK^2-4a^2\) (1)
Mặt khác: \(\dfrac{1}{BK^2}=\dfrac{1}{BM^2}+\dfrac{1}{BD^2}\Rightarrow\dfrac{1}{BK^2}-\dfrac{1}{BD^2}=\dfrac{1}{3a^2}\) (2)
(1);(2) \(\Rightarrow\left\{{}\begin{matrix}BD^2=8BK^2-4a^2\\\dfrac{1}{BK^2}-\dfrac{1}{BD^2}=\dfrac{1}{3a^2}\end{matrix}\right.\)
\(\Rightarrow\dfrac{8}{BD^2+4a^2}-\dfrac{1}{BD^2}=\dfrac{1}{3a^2}\Rightarrow BD\Rightarrow SH\)
Sao kết quả xấu vậy nhỉ?