Giải Hệ Phương Trình {(-1)a + b = 6 {2a + b = -3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt S=x+y, P=x.y
Ta có:S=2a-1, x^2+y^2=S^2-2P=a^2+2a-3
\Rightarrow P=\frac{1}{2}[(2a-1)^2-(a^2+2a-3)]=\frac{1}{2}(3a^2-6a+4)
Trước hết tìm a để hệ có nghiệm.
Điều kiện để hệ có nghiệm:S^2-4P \geq 0 \Leftrightarrow (2a-1)^2-2(3a^2-6a+4)\geq 0
\Leftrightarrow -2a^2+8a-7 \geq 0 \leftrightarrow 2-\frac{\sqrt{2}}{2} \leq a \leq 2+\frac{\sqrt{2}}{2} (1)
Tìm a để P=\frac{1}{2}(3a^2-6a+4) đạt giá trị nhỏ nhất trên đoạn
[2-\frac{\sqrt{2}}{2} ;2+\frac{\sqrt{2}}{2}]
Ta có hoành độ đỉnh a_0=\frac{6}{2.3}=1Parabol có bề lõm quay lên do đó \min P=P(2-\frac{\sqrt{2}}{2} )$
Vậy với a=2-\frac{\sqrt{2}}{2} thì xy đạt giá trị nhỏ nhất.
cho hệ phương trình{6x+ay=6 và 2ax+by=3
- giải hệ phương trình khi a=b=1
- tìm a,b để hệ có nghiệm x=1,y=5

6x+ay=6, 2ax+by=3
Thay a=b=1 vào hệ phương trình ta có 6x+y=6, 2x+y=3
6x+y-(2x+y)=6-3
4x=3
x=3/4
y=6-6.3/4=3/2
Vì hệ có nghiệm x=1,y=5 nên ta có 6.1+a.5=6 và 2a+5b=3
a.5=0
a=0
Thay a=0 vào 2a+5b=3 ta có 0+5b=3 =>b=3/5

Cách 1
Ta có: 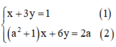
Từ (1) rút ra được x = 1 – 3y (*)
Thay vào phương trình (2) ta được :
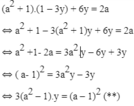
a) a = -1, phương trình (**) trở thành : 0y = 4
Phương trình trên vô nghiệm
Vậy hệ phương trình khi a = -1 vô nghiệm.
b) a = 0, phương trình (**) trở thành -3y = 1 ⇔
Thay 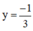 vào (*) ta được x = 2.
vào (*) ta được x = 2.
Vậy hệ phương trình khi a = 0 có nghiệm duy nhất 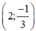
c) a = 1, phương trình (**) trở thành: 0y = 0
Phương trình nghiệm đúng với mọi y.
Vậy hệ phương trình khi a = 1 có vô số nghiệm dạng (1 – 3y; y) (y ∈ R).
Cách 2
a) Thay a = -1 vào hệ phương trình ta được hệ phương trình mới:

Vậy hệ phương trình vô nghiệm khi a= - 1.
b) Thay a = 0 vào hệ phương trình ta được hệ phương trình mới:

c) Thay a=1 vào hệ phương trình ta được hệ phương trình mới:
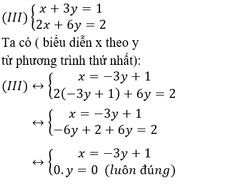
Vậy với a= 1 hệ phương trình có vô số nghiệm với nghiệm tổng quát là (-3y+1;y),(y ∈ R)
Kiến thức áp dụng
+ Giải hệ phương trình 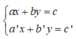 ta làm như sau:
ta làm như sau:
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
+ Nếu xuất hiện phương trình dạng 0x = a (hoặc 0y = a) thì ta kết luận hệ phương trình vô nghiệm nếu a ≠ 0 hoặc hệ có vô số nghiệm nếu a = 0.

Đáp án B
Do hệ phương trình đã cho có nghiệm là (1; 1) nên:
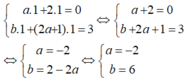
Vậy a = -2; b = 6

Bài 2:
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(2x^2=-x+3\)
\(\Leftrightarrow2x^2+x-3=0\)
\(\Leftrightarrow2x^2-2x+3x-3=0\)
\(\Leftrightarrow2x\left(x-1\right)+3\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Thay x=1 vào hàm số \(y=2x^2\), ta được:
\(y=2\cdot1^2=2\)
Thay \(x=-\dfrac{3}{2}\) vào hàm số \(y=2x^2\), ta được:
\(y=2\cdot\left(-\dfrac{3}{2}\right)^2=2\cdot\dfrac{9}{4}=\dfrac{9}{2}\)
Vậy: Tọa độ giao điểm của (p) và (D) là (1;2) và \(\left(-\dfrac{3}{2};\dfrac{9}{2}\right)\)



\(\left\{{}\begin{matrix}-a+b=6\\2a+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a=-9\\-a+b=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=3\end{matrix}\right.\)
\(\left\{{}\begin{matrix}-a+b=6\\2a+b=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-a+b=6\\-a+b-2a-b=6-\left(-3\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-a+b=6\\-3a=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-\left(-3\right)+b=6\\a=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=3\\a=-3\end{matrix}\right.\)