cho tỉ lệ thức a/b=c/d chứng minh (a+b/c+d)^2=a^2+b^2/c^2+d^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lần sau bạn cho thêm cả dấu ngoặc cho dễ hiểu nhé :v
Đặt \(\frac{a}{b}=\frac{c}{d}=k\) => \(\left\{{}\begin{matrix}a=b.k\\c=d.k\end{matrix}\right.\) \(\left(b,d\ne0\right)\)
Thay \(\left\{{}\begin{matrix}a=b.k\\c=d.k\end{matrix}\right.\) vào \(\frac{a^2-b^2}{ab}\) và \(\frac{c^2-d^2}{cd}\) ta có :
\(\left\{{}\begin{matrix}\frac{\left(b.k\right)^2-b^2}{b.k.b}\\\frac{\left(d.k\right)^2-d^2}{d.k.d}\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}\frac{b^2.k^2-b^2}{b^2.k}\\\frac{d^2.k^2-d^2}{d^2.k}\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}\frac{b^2\left(k^2-1\right)}{b^2.k}\\\frac{d^2\left(k^2-1\right)}{d^2.k}\end{matrix}\right.\) <=>\(\left\{{}\begin{matrix}\frac{k^2-1}{k}\\\frac{k^2-1}{k}\end{matrix}\right.\)(vì b,d khác 0 nên \(b^2,d^2\) khác 0)
=> \(\frac{a^2-b^2}{ab}\) = \(\frac{c^2-d^2}{cd}\) (vì cùng bằng \(\frac{k^2-1}{k}\))
vậy \(\frac{a^2-b^2}{ab}\) = \(\frac{c^2-d^2}{cd}\) nếu \(\frac{a}{b}=\frac{c}{d}\)
lâu lắm không làm nên không chắc đâu :v

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=>a=bk; c=dk
(a+2c)(b+d)=(bk+2dk)(b+d)=k(b+2d)(b+d)
(a+c)(b+2d)=(bk+dk)(b+2d)=k(b+2d)(b+d)
Do đó: VT=VP(đpcm)

(a² + b²) / (c² + d²) = ab/cd
<=> (a² + b²)cd = ab(c² + d²)
<=> a²cd + b²cd = abc² + abd²
<=> a²cd - abc² - abd² + b²cd = 0
<=> ac(ad - bc) - bd(ad - bc) = 0
<=> (ac - bd)(ad - bc) = 0
<=> ac - bd = 0 hoặc ad - bc = 0
<=> ac = bd hoặc ad = bc
<=> a/b = d/c hoặc a/b = c/d (đpcm)

Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk; c=dk$. Khi đó:
$\frac{ab}{cd}=\frac{bk.b}{dk.d}=\frac{b^2}{d^2}(1)$
$\frac{a^2-b^2}{c^2-d^2}=\frac{(bk)^2-b^2}{(dk)^2-d^2}=\frac{b^2(k^2-1)}{d^2(k^2-1)}=\frac{b^2}{d^2}(2)$
Từ $(1); (2)$ ta có đpcm
------------------------
Lại có:
$(\frac{a+b}{c+d})^2=(\frac{bk+b}{dk+d})^2=(\frac{b(k+1)}{d(k+1)})^2=(\frac{b}{d})^2(3)$
$\frac{a^2+b^2}{c^2+d^2}=\frac{(bk)^2+b^2}{(dk)^2+d^2}=\frac{b^2(k^2+1)}{d^2(k^2+1)}=\frac{b^2}{d^2}=(\frac{b}{d})^2(4)$
Từ $(3); (4)$ ta có đpcm.


Đặt ab=cd=kab=cd=k
Khi đó ta có :
a=bka=bk và c=dkc=dk
Suy ra :
a2−b2c2−d2=(bk)2−b2(dk)2−d2a2-b2c2-d2=(bk)2-b2(dk)2-d2
=b2k2−b2d2k2−d2=b2k2-b2d2k2-d2
=b

ban coi trong sach giao khoa ti le thuc se co mot phan chung minh cho ban thay bang cach dat a/b=c/d=k nha
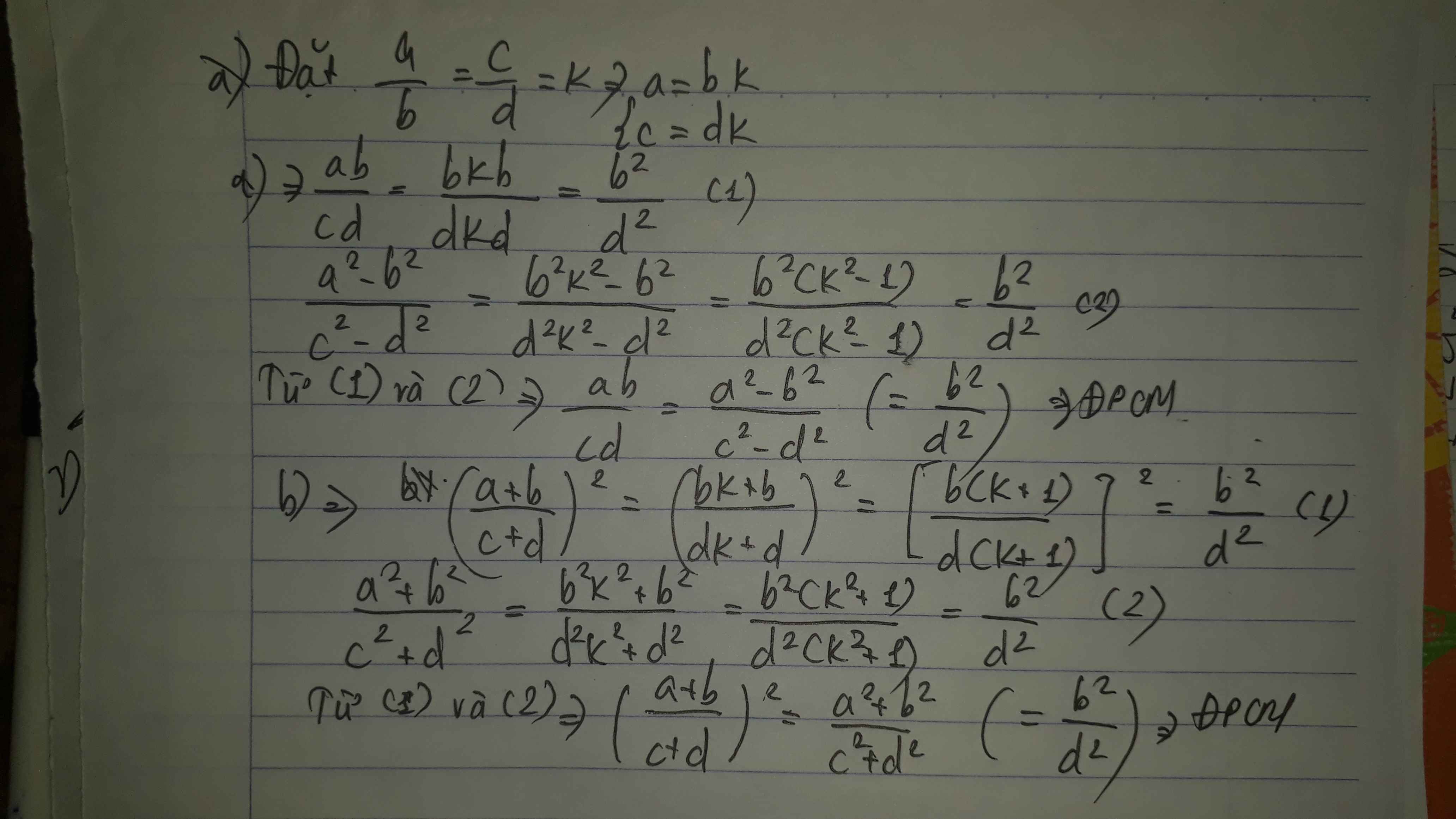
Có \(\frac{a}{b}=\frac{c}{d}=\frac{a}{c}=\frac{b}{d}\)
Theo tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\)
\(=\left(\frac{a}{c}\right)^2=\left(\frac{b}{d}\right)^2=\left(\frac{a+b}{c+d}\right)^2\)
\(=\frac{a^2}{c^2}=\frac{b^2}{d^2}=\left(\frac{a+b}{c+d}\right)^2\)
Có \(\frac{a^2}{c^2}=\frac{b^2}{d^2}\)
Theo dãy tính chất tỉ số bằng nhau ta có :
\(\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2+b^2}{c^2+d^2}\)
Từ (1) và (2) = \(\left(\frac{a+b}{c+d}\right)^2=\frac{a^2+b^2}{c^2+d^2}\)