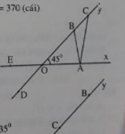
Cho góc nhọn xOy trên tia Ox ta lấy 4 điểm phân biệt A, B, C, D trên tia Oy ta lấy 5 điểm phân biệt E, F, G, H,K . Hỏi từ 10 điểm , ta có bao nhiêu tam giác tạo thành ( chọn 3 điểm để tạo thành 1 tam giác )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 3 2023
\(\text{#TuanNam}\)
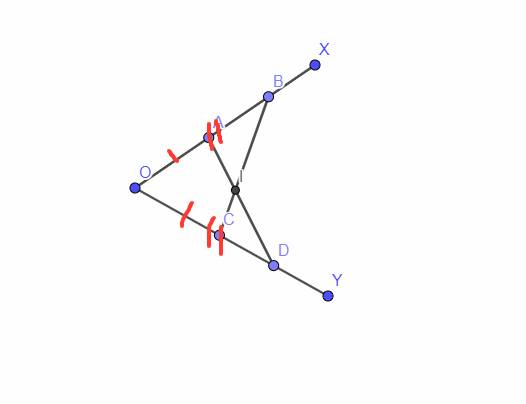
`a,` Mình xp sửa đề câu a: cm: Tam giác `OAD =` Tam giác `OCB (` vì nếu là `OCD` thì k đúng, vì `3` điểm đó thẳng hàng `)`.
Xét Tam giác `OAD` và Tam giác `OCB` có:
`OA=OC (g``t)`
\(\widehat{O}\) chung
`OB=OD (g``t)`
`=>` Tam giác `OAD =` Tam giác `OCB (c-g-c)`
`b,` Hnhu đề bị sai ;-;
`
25 tháng 8 2018
Các tam giác phải đếm gồm ba loại:
- Loại 1: Các tam giác có một đỉnh là O, đỉnh thứ hai là một trong ba điểm A, B, C (có 3 cách chọn), đỉnh thứ ba là một trong bốn điểm D, E, G, H (có 4 cách chọn). Các tam giác loại 1 gồm: 3 . 4 = 12 (tam giác).
mk ko bt vẽ hình trên này thế nào nên mk ko vẽ hình đôu
k mk nha
25 tháng 8 2018
ok. mk sẽ kết bạn. nhưng cậu mới làm được có 1 loại còn 2 loại thì sao?
CM
4 tháng 10 2019
Đáp án A
Số cách chọn 3 điểm bất kì là C 30 3
Để 3 điểm đó lập thành một tam giác thì 3 điểm đó không thẳng hàng
Số cách chọn 1 điểm thuộc d 1
2 điểm thuộc d 2 : C 10 1 . C 20 2
Số cách chọn 2 điểm thuộc d 1
1 điểm thuộc d 2 : C 10 2 . C 20 1
Xác suất để 3 điểm chọn được tạo thành tam giác là
CM
11 tháng 7 2018
Đáp án A
Số cách chọn 3 điểm bất kì là: C 30 3
Để 3 điểm đó lập thành một tam giác thì 3 điểm đó không thẳng hàng:
Số cách chọn 1 điểm thuộc d 1 , 2 điểm thuộc d 2 : C 10 1 . C 20 2
Số cách chọn 2 điểm thuộc d 1 , 1 điểm thuộc d 2 : C 10 2 . C 20 1
Xác suất để 3 điểm chọn được tạo thành tam giác là: C 10 1 C 20 2 + C 10 2 C 20 1 C 30 3
CM
20 tháng 12 2018
Đáp án A
Số cách chọn 3 điểm bất kì là: C 30 3
Để 3 điểm đó lập thành một tam giác thì 3 điểm đó không thẳng hàng:
Số cách chọn 1 điểm thuộc d 1 , 2 điểm thuộc d 2 : C 10 1 . C 20 2
Số cách chọn 2 điểm thuộc d 1 , 1 điểm thuộc d 2 : C 10 2 . C 20 1
Xác suất để 3 điểm chọn được tạo thành tam giác là: C 10 1 C 20 2 + C 10 2 C 20 1 C 30 3