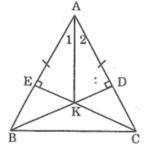
Cho tam giác ABC cân tại A góc A < 90* , kẻ BD vuông góc với AC và CE vuông góc với AB . Chứng minh
Tam giác ABD bằng tam giác ACE
K là giao của BD và CE chứng minh AK là phân gác của góc BAC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 3 2016
Xét T.giác ABD và T.giác ACE có:
AB=AC (tam giác ABC cân)
góc A: góc chung
AE=AD
Do đó: t.giác ABD = t.giác ACE ( c-g-c)
17 tháng 2 2022
a: Xét ΔBEC vuông tại E và ΔCDB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó: ΔBEC=ΔCDB
b: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
BD=CE
Do đó: ΔABD=ΔACE
Xét ΔBEK vuông tại E và ΔCDK vuông tại D có
EB=DC
\(\widehat{EBK}=\widehat{DCK}\)
Do đó: ΔBEK=ΔCDK
c: Xét ΔBAK và ΔCAK có
BA=CA
AK chung
BK=CK
Do đó: ΔBAK=ΔCAK
Suy ra: \(\widehat{BAK}=\widehat{CAK}\)
hay AK là tia phân giác của góc BAC
CM
28 tháng 8 2017
Xét ΔADB vuông tại D và ΔAEC vuông tại E, ta có:
AB = AC (giả thiết)
∠(BAC) chung
⇒ ΔADB = ΔAEC (cạnh huyền, góc nhọn)
⇒ AD = AE (hai cạnh tương ứng)
Xét ΔADK vuông tại D và ΔAEK vuông tại E có:
AD = AE (chứng minh trên)
AK cạnh chung
⇒ ΔADK = ΔAEK (cạnh huyền, cạnh góc vuông)
⇒ ∠(DAK) = ∠(EAK) (hai góc tương ứng)
Vậy AK là tia phân giác của góc BAC.
5 tháng 8 2023
a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
góc EBC=góc DCB
=>ΔEBC=ΔDCB
b: Xét ΔKEB vuông tại E và ΔKDC vuông tại D có
EB=DC
góc KBE=góc KCD
=>ΔKEB=ΔKDC
c: Xét ΔAEK vuông tại E và ΔADK vuông tại D có
AK chung
KE=KD
=>ΔAEK=ΔADK
=>góc EAK=góc DAK
=>AK là phân giác của góc BAC
d: ΔABC cân tại A có AK là phân giác
nên AK là trung trực của BC
=>A,K,I thẳng hàng
28 tháng 4 2023
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
góc A chung
=>ΔADB=ΔAEC
=>góc ABD=góc ACE
b: góc HBC+góc ABD=góc ABC
góc HCB+góc ACE=góc ACB
mà góc ABD=góc ACE; góc ABC=góc ACB
nên góc HBC=góc HCB
=>ΔBHC cân tại H
=>HB=HC>HD
7 tháng 1 2016
Tự vẽ hình nha bạn
Ta có: tam giác ABC cân tại A
=> B = C
Ta có: Góc D = góc E = 90o (góc vuông)
K1 = K2 (2 góc đối đỉnh)
=> 180 - E - K1 = 180 - D - K2
=> B1 = C1
Vì B = C ; B1 = C1 => B - B1 = C - C1
=> B2 = C2
Vì B2 = C2 nên KBC cân tại K
=> KB = KC
Xét tam giác AKB và tam giác AKC có:
AK cạnh chung (1)
AB = AC (2)
BK = BC (3)
Từ (1) ; (2) ; (3) = > Tam giác AKB = tam giác AKC (c - c - c) (4)
Từ (4) = > A1 = A2 (2 góc tương ứng)
=> AK là tia phân giác của góc A
=> ĐPCM
Tớ sẽ bổ sung thêm hình sau
HN
22 tháng 5 2017
Xét hai tam giác ADB và AEC có:
AB = AC (do \(\Delta ABC\) cân tại A)
\(\widehat{A}\): góc chung
Vậy: \(\Delta ADB=\Delta AEC\left(ch-gn\right)\)
Suy ra: AD = AE (hai cạnh tương ứng)
Xét hai tam giác vuông ADK và AEK có:
AK: cạnh huyền chung
AD = AE (cmt)
Vậy: \(\Delta ADK=\Delta AEK\left(ch-cgv\right)\)
Suy ra: \(\widehat{A_1}=\widehat{A_2}\) (hai góc tương ứng)
Do đó: AK là tia phân giác của góc A.
31 tháng 1 2019
Giải
Xét tam giác EBC và tam giác DBC có:
E=D=90
B=C(gt)
BC là cạnh chung
=>tam giacs EBC=tam giác DBC( cạnh huyền-góc nhọn)
=>EC=DB( 2 cạnh TƯ)
Xét tam giác AEC và tam giác ADB có;
AB=AC(gt)
EC=BK(cmt)
AK cạnh chung
=> tam giác AEC=tam giác ADB(c.c.c)
=>B1=C1
Xét tam giác ABKvaf tam giác ACK có
AB=AC(gt)
AK chung
B1=C1(cmt)
=>tam giavs ABK=tam giác ACK(c.g.c)
=>A1=A2
=>AK là tia pg của góc A
(cmt: chứng minh trên)
16 tháng 4 2022
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đo: ΔABD=ΔACE
b: Xét ΔAEI vuông tại E và ΔADI vuông tại D có
AI chung
AE=AD
Do đó: ΔAEI=ΔADI
Suy ra: \(\widehat{EAI}=\widehat{DAI}\)
hay AI là tia phân giác của góc BAC
Ta có: ΔABC cân tại A
mà AH là đường phân giác
nên AH là đường cao
26 tháng 1 2022
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
Suy ra: BD=CE
b: Xét ΔAED có AE=AD
nên ΔAED cân tại A
c: Xét ΔEBI vuông tại E và ΔDCI vuông tại D có
EB=DC
\(\widehat{EBI}=\widehat{DCI}\)
Do đó; ΔEBI=ΔDCI
Suy ra: IB=IC
Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC