Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A)Dựa vào tính chất của dãy tỉ số bằng nhau:
x/1 = y/2 = z/3 = 4x -3y +2z /4.1 -3.2 +2.3 =36/4 =9
x/1=9 =>x=9.1=9
y/2=9=>y=9.2=18
z/3=9=>z=9.3=27
B)Dựa vào tính chất của dãy tỉ số bằng nhau:
x/3=y/8=z/5=3x+y-2z/3.3+8-2.5=14/7=2
x/3=2=>x=2.3=6
y/8=2=>y=2.8=16
z/5=2=>z=2.5=10
C)Dựa vào tính chất của dãy tỉ số bằng nhau:
x/3=y/8=z/5=2y+3y-z/2.3+3.8-5=50/25=2
x/3=2=>x=2.3=6
y/8=2=>y=2.8=16
z/5=2=>z=2.5=10
A)Dựa vào tính chất của dãy tỉ số bằng nhau:
x/1 = y/2 = z/3 = 4x -3y +2z /4.1 -3.2 +2.3 =36/4 =9
x/1=9 =>x=9.1=9
y/2=9=>y=9.2=18
z/3=9=>z=9.3=27
B)Dựa vào tính chất của dãy tỉ số bằng nhau:
x/3=y/8=z/5=3x+y-2z/3.3+8-2.5=14/7=2
x/3=2=>x=2.3=6
y/8=2=>y=2.8=16
z/5=2=>z=2.5=10
C)Dựa vào tính chất của dãy tỉ số bằng nhau:
x/3=y/8=z/5=2y+3y-z/2.3+3.8-5=50/25=2
x/3=2=>x=2.3=6
y/8=2=>y=2.8=16
z/5=2=>z=2.5=10

Ta có : \(\frac{x}{5}=y=\frac{z}{-2}\Rightarrow\frac{x}{5}=\frac{y}{1}=\frac{z}{-2}\Rightarrow\frac{x}{5}=\frac{y}{1}=\frac{2z}{-4}\)
Lại có : -x - y + 2z = 160
=> -(x + y - 2z) = 160
=> x + y - 2z = -160
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{5}=\frac{y}{1}=\frac{2z}{-4}=\frac{x+y-2z}{5+1-\left(-4\right)}=\frac{-160}{10}=-16\)
=> x = -16.5 = -80 , y = -16 , z = -16.(-2) = 32
Đặt \(\frac{x}{3}=\frac{y}{8}=\frac{z}{5}=k\Rightarrow\hept{\begin{cases}x=3k\\y=8k\\z=5k\end{cases}}\)
=> 4x = 12k , 3y = 24k , 2z = 10k
=> 4x + 3y - 2z = 12k + 24k - 10k
=> 52 = 26k
=> k = 2
Với k = 2 thì x = 3.2 = 6 , y = 8.2 = 16 , z= 5.2 = 10
8x = 5y => \(\frac{x}{5}=\frac{y}{8}\)
=> \(\frac{2x}{10}=\frac{y}{8}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{2x}{10}=\frac{y}{8}=\frac{y-2x}{8-10}=\frac{-10}{-2}=5\)
=> x = 5.5 = 25,y = 5.8 = 40

b) Đặt \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2k\\y=3k\\z=4k\end{matrix}\right.\)
Ta có: \(x^2-y^2+2z^2=108\)
\(\Leftrightarrow\left(2k\right)^2-\left(3k\right)^2+2\cdot\left(4k\right)^2=108\)
\(\Leftrightarrow4k^2-9k^2+2\cdot16k^2=108\)
\(\Leftrightarrow k^2=4\)
Trường hợp 1: k=2
\(\Leftrightarrow\left\{{}\begin{matrix}x=2k=2\cdot2=4\\y=3k=3\cdot2=6\\z=4k=4\cdot2=8\end{matrix}\right.\)
Trường hợp 2: k=-2
\(\Leftrightarrow\left\{{}\begin{matrix}x=2k=2\cdot\left(-2\right)=-4\\y=3k=3\cdot\left(-2\right)=-6\\z=4k=4\cdot\left(-2\right)=-8\end{matrix}\right.\)

Ta có: \(\dfrac{x}{y}=\dfrac{7}{20}\)
nên \(\dfrac{x}{7}=\dfrac{y}{20}\)(1)
Ta có: \(\dfrac{y}{z}=\dfrac{5}{8}\)
nên \(\dfrac{y}{5}=\dfrac{z}{8}\)
hay \(\dfrac{y}{20}=\dfrac{z}{32}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{7}=\dfrac{y}{20}=\dfrac{z}{32}\)
hay \(\dfrac{2x}{14}=\dfrac{5y}{100}=\dfrac{2z}{64}\)
mà 2x-5y+2z=100
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{14}=\dfrac{5y}{100}=\dfrac{2z}{64}=\dfrac{2x-5y+2z}{14-100+64}=\dfrac{100}{-22}=\dfrac{-50}{11}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{7}=\dfrac{-50}{11}\\\dfrac{y}{20}=\dfrac{-50}{11}\\\dfrac{z}{32}=-\dfrac{50}{11}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{350}{11}\\y=\dfrac{-1000}{11}\\z=\dfrac{-1600}{11}\end{matrix}\right.\)
Ta có: \(\dfrac{x}{y}=\dfrac{7}{20}\Rightarrow\dfrac{x}{7}=\dfrac{y}{20}\Rightarrow\dfrac{x}{14}=\dfrac{y}{40}\Rightarrow\dfrac{2x}{28}=\dfrac{5y}{200}\) \(\left(1\right)\)
Lại có: \(\dfrac{y}{z}=\dfrac{5}{8}\Rightarrow\dfrac{y}{5}=\dfrac{z}{8}\Rightarrow\dfrac{y}{40}=\dfrac{z}{64}\Rightarrow\dfrac{5y}{200}=\dfrac{2z}{128}\) \(\left(2\right)\)
Kết hợp ( 1 ) và ( 2 ) ta có: \(\dfrac{2x+5y-2z}{28+200-128}=\dfrac{100}{100}=1\)
⇒ \(\dfrac{2x}{28}=1\Rightarrow x=\dfrac{1.28}{2}=14\)
⇒ \(\dfrac{5y}{200}=1\Rightarrow y=\dfrac{1.200}{5}=40\)
⇒ \(\dfrac{2z}{128}=1\Rightarrow z=\dfrac{1.128}{2}=64\)

a) Từ \(\dfrac{x}{y}=\dfrac{9}{7}\Rightarrow\dfrac{x}{9}=\dfrac{y}{7}\) (1)
Từ \(\dfrac{y}{z}=\dfrac{7}{3}\Rightarrow\dfrac{y}{7}=\dfrac{z}{3}\) (2)
Từ (1) và (2) =>\(\dfrac{x}{9}=\dfrac{y}{7}=\dfrac{z}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\dfrac{x}{9}=\dfrac{y}{7}=\dfrac{z}{3}=\dfrac{x-y+z}{9-7+3}=\dfrac{-15}{5}=-3\)
\(\Rightarrow\left\{{}\begin{matrix}x=-3\cdot9\\y=-3\cdot7\\z=-3\cdot3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-27\\y=-21\\z=-9\end{matrix}\right.\)
b) Từ \(\dfrac{x}{y}=\dfrac{7}{20}\Rightarrow\dfrac{x}{7}=\dfrac{y}{20}\) (1)
Từ \(\dfrac{y}{z}=\dfrac{5}{8}\Rightarrow\dfrac{y}{5}=\dfrac{z}{8}\Rightarrow\dfrac{y}{20}=\dfrac{z}{32}\) (2)
Từ (1) và (2) =>\(\dfrac{x}{7}=\dfrac{y}{20}=\dfrac{z}{32}=\dfrac{2x}{14}=\dfrac{5y}{100}=\dfrac{2z}{64}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\dfrac{x}{7}=\dfrac{y}{20}=\dfrac{z}{32}=\dfrac{2x}{14}=\dfrac{5y}{100}=\dfrac{2z}{64}=\dfrac{2x+5y-2z}{14+100-64}=\dfrac{100}{50}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\cdot7\\y=2\cdot20\\z=2\cdot32\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=14\\y=40\\z=64\end{matrix}\right.\)
c) Đặt \(\dfrac{x}{12}=\dfrac{y}{9}=\dfrac{z}{5}=k\)
=> \(x=12k\) ; \(y=9k\) ;\(z=5k\)
=> xyz = \(12k\cdot9k\cdot5k\) =\(540\cdot k^3\) = 20
=>\(k^3=20:540=\dfrac{1}{27}=\left(\dfrac{1}{3}\right)^3\)
=>\(k=\dfrac{1}{3}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}\cdot12\\y=\dfrac{1}{3}\cdot9\\z=\dfrac{1}{3}\cdot5\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=4\\y=3\\z=\dfrac{5}{3}\end{matrix}\right.\)
d) Từ \(\dfrac{x}{5}=\dfrac{y}{7}=\dfrac{z}{3}\Rightarrow\dfrac{x^2}{25}=\dfrac{y^2}{49}=\dfrac{z^2}{9}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\dfrac{x^2}{25}=\dfrac{y^2}{49}=\dfrac{z^2}{9}=\dfrac{x^2+y^2+z^2}{25+49+9}=\dfrac{585}{83}\)
\(\Rightarrow\left\{{}\begin{matrix}x^2=\dfrac{585}{83}\cdot25\\y^2=\dfrac{585}{83}\cdot49\\z^2=\dfrac{585}{83}\cdot9\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x^2=\\y^2=\\z^2=\end{matrix}\right.\) đề bài sai nên ko tìm được x ; y ; z

Câu a) sai đề nhé bạn.
b) Ta có:
\(\frac{x}{y}=\frac{7}{20};\frac{y}{z}=\frac{5}{8}\) và \(2x+5y-2z=100\)
\(\Rightarrow\frac{x}{7}=\frac{y}{20};\frac{y}{5}=\frac{z}{8}\Leftrightarrow\frac{x}{7}=\frac{y}{20}=\frac{z}{32}\) và \(2x+5y-2z=100\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{x}{7}=\frac{y}{20}=\frac{z}{32}=\frac{2x+5y-2z}{2.7+5.20-2.32}=\frac{100}{50}=2\)
\(\hept{\begin{cases}\frac{x}{7}=2\Rightarrow x=2.7=14\\\frac{y}{20}=2\Rightarrow y=2.20=40\\\frac{z}{32}=2\Rightarrow z=2.32=64\end{cases}}\)
Vậy \(x=14;y=40;z=64\)
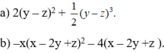
\(\frac{x}{3}\)=\(\frac{y}{8}\)=\(\frac{z}{5}\)=\(\frac{2x}{6}\)=\(\frac{2z}{10}\)=\(\frac{2x+y-2z}{6+8-10}\)=\(\frac{12}{4}\)=3