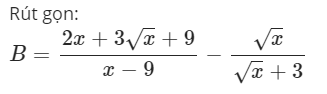
@Nguyễn Lê Phước Thịnh: NÉ HỘ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bạn ghi rõ nội dung, yêu cầu đề của bài đó ra cho mình nha

b) Ta có: \(\left(-\dfrac{1}{2}\right)^2\cdot2\dfrac{6}{7}-\dfrac{14}{15}:2\dfrac{1}{3}+\left(-1.21\right)^0\)
\(=\dfrac{1}{4}\cdot\dfrac{20}{7}-\dfrac{14}{15}:\dfrac{7}{3}+1\)
\(=\dfrac{5}{7}-\dfrac{14}{15}\cdot\dfrac{3}{7}+1\)
\(=\dfrac{5}{7}-\dfrac{2}{5}+1\)
\(=\dfrac{25-14-35}{35}=\dfrac{-24}{35}\)

b: \(\Leftrightarrow n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{0;-2;1;-3;3;-5\right\}\)
c: \(\Leftrightarrow n+2\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{-1;-3;3;-7\right\}\)
d: \(\Leftrightarrow n+2\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{-1;-3;0;-4;2;-6\right\}\)
a: \(\Leftrightarrow n-1\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{2;0;6;-4\right\}\)

\(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{2021}{2022}\cdot\dfrac{2022}{2023}\)
=1/2023
\(B=\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{3}{4}...\dfrac{2021}{2022}.\dfrac{2022}{2023}\)
\(=\dfrac{1.2.3...2022}{2.3.4...2023}=\dfrac{1}{2023}\)

a: \(A=\left(b^2+c^2-a^2\right)^2-4b^2c^2\)
\(=\left(b^2+c^2-a^2\right)^2-\left(2bc\right)^2\)
\(=\left(b^2-2bc+c^2-a^2\right)\left(b^2+2bc+c^2-a^2\right)\)
\(=\left[\left(b+c\right)^2-a^2\right]\left[\left(b-c\right)^2-a^2\right]\)
\(=\left(b+c-a\right)\left(b+c+a\right)\left(b-c-a\right)\left(b-c+a\right)\)
b: a,b,c là độ dài 3 cạnh của 1 tam giác
=>b+c>a và a+b>c và a+c>b
=>b+c-a>0 và a+b-c>0 và a+c-b>0
=>b+c-a>0 và b-(c+a)<0 và a+b-c>0
=>(b+c-a)[b-(c+a)][a+b-c](a+b+c)<0
=>A<0

\(B=\dfrac{2x+3\sqrt{x}+9}{x-9}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(\Rightarrow B=\dfrac{2x+3\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{2x+3\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{2x+3\sqrt{x}+9-x+3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{x+6\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{\left(\sqrt{x}+3\right)^2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\)
\(\dfrac{2x+3\sqrt{x}+9-\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\left(\sqrt{x}+3\right)^2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\)