Một vật ở mặt đất có trọng lượng 20N. Hỏi phải đưa vật đến độ cao nào so với bề mặt Trái Đất thì trọng lượng bằng 10N. Biết bán kính Trái Đất bằng 6400 km. Tìm độ cao vật.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án B
+ Gia tốc rơi tự do ở độ cao h: 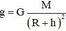
+ Gia tốc rơi tự do ở mặt đất:
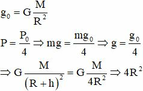
![]()
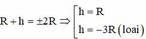
![]()

Ta có:
Trọng lượng của vật ở mặt đất:
P = G m M R 2
Trọng lượng của vật ở độ cao h:
P h = G m M R + h 2
Theo đề bài, ta có:
P h = 0 , 4 P ↔ G m M R + h 2 = 0 , 4 G m M R 2 ↔ R 2 = 0 , 4 R + h 2 → h = 0 , 581 R = 0 , 581.6400 = 3718 , 4 k m
Đáp án: B

\(\dfrac{P}{P'}=\dfrac{G\cdot\dfrac{M\cdot m}{R^2}}{G\cdot\dfrac{M\cdot m}{\left(R+h\right)^2}}=\dfrac{\dfrac{1}{R^2}}{\dfrac{1}{\left(R+0,5R\right)^2}}=\dfrac{9}{4}\)
\(\Rightarrow P'=\dfrac{P\cdot4}{9}=\dfrac{45\cdot4}{9}=20\left(N\right)\)

Ta có
Trọng lượng của vật ở mặt đất:
P = G m M R 2
Trọng lượng của vật ở độ cao h
P h = G m M R + h 2
Theo đề bài, ta có:
P h = 2 3 P ↔ G M m ( R + h ) 2 = 2 3 G M m R 2
⇔ 2 3 ( R + h ) 2 = R 2 ⇒ h = 0,225 R = 0,225.6400 = 1440 k m
Đáp án: C

1/
Trọng lực ở đây đóng vai trò như 1 lực hấp dẫn
Theo đề ta có trọng lượng của quả cầu ở độ cao h bằng 1/4 trọng lượng của nó trên mặt đất
\(P'=\dfrac{1}{4}\cdot P\Rightarrow G\cdot\dfrac{mM}{\left(R+h\right)^2}=\dfrac{1}{4}\cdot G\cdot\dfrac{mM}{R^2}\)
\(\Rightarrow\dfrac{1}{\left(6400\cdot1000+h\right)^2}=\dfrac{1}{4\cdot\left(6400\cdot1000\right)^2}\Rightarrow h=6400000\left(m\right)=6400\left(km\right)\)
ChọnC
2/
Theo đề ta có gia tốc rơi tự do có giá trị bằng 1/3 gia tốc rơi tự do ở mặt đất ở độ cao
\(g'=\dfrac{1}{3}g\Rightarrow G\dfrac{M}{\left(R+h\right)^2}=\dfrac{1}{3}\cdot G\dfrac{M}{R^2}\)
\(\Rightarrow\dfrac{1}{\left(6400\cdot1000+h\right)^2}=\dfrac{1}{3\cdot\left(6400\cdot1000\right)^2}\Rightarrow h=4685125,168\left(m\right)\approx4685\left(km\right)\)
Chọn B
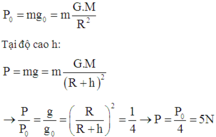
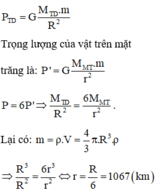
Ta có :
\(\frac{\text{P}_đ}{\text{P}_{\text{h}}}=\frac{\text{mg}_đ}{\text{mg}_{\text{h}}}=\frac{\text{g}_đ}{\text{g}_{\text{h}}}=\frac{\text{GM}\div\text{R}^2}{\text{GM}\div\left(\text{R}+\text{h}\right)^2}=\left(\frac{\text{R}+\text{h}}{\text{R}}\right)^2\)
\(\Rightarrow\frac{20}{10}=\left(\frac{6400+\text{h}}{6400}\right)^2\)
\(\Rightarrow\sqrt{2}=\frac{6400+\text{h}}{6400}\)
\(\Rightarrow\text{h}=2651\text{ km}\)