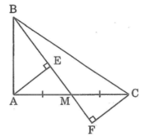
Cho tam giác ABC vuông tại A,AB=3cm. M là trung điểm AC. Gọi AE,CF là các đường vuông góc kẻ từ A,C đến đường thẳng BM.C/m:
a)ME=MF
b)BE+BF>6cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 3 2019
Xét tam giác AEM và tam giác CFM có:
\(\widehat{AEM}=\widehat{CFM}=90^o\)
AM=MC( M là trung điểm AC)
\(\widehat{AME}=\widehat{CMF}\)( đối đỉnh)
=> tam giác AEM=CFM
=> ME=MF
b) BE+BF=BE+BM+MF=BE+BM+EM=(BE+EM)+BM=BM+BM=2.BM
Xét tam giác BAM vuông tại A
=> BM>AB
=> BE+BF=2.BM>2.AB>2.3=6
=> dpcm
24 tháng 7 2023
a: Xét ΔMEA vuông tại E và ΔMFC vuông tại F có
MA=MC
góc AME=góc CMF
=>ΔMEA=ΔMFC
=>ME=MF
b: BE+BF
=BE+BE+EF
=BE+BE+2*ME
=2*BE+2*ME
=2*BM
c: ΔAMB vuông tại A
=>AB<BM
CM
4 tháng 10 2017
Trong ΔABM, ta có ∠(BAM) = 90o
Suy ra: AB < BM (trong tam giác vuông cạnh huyền lớn nhất)
Mà BM = BE + EM = BF - MF
Suy ra: AB < BE + EM
AB < BF - FM
Suy ra:AB + AB < BE + ME + BF - MF (1)
Xét hai tam giác vuông AEM và CFM, ta có:
∠(AEM) = ∠(CFM) = 90o
AM = CM (gt)
∠(AME) = ∠(CMF) (đối đỉnh)
Suy ra: ΔAEM = ΔCFM (cạnh huyền - góc nhọn)
Suy ra: ME = MF (2)
Từ (1) và (2) suy ra: AB + AB < BE + BF
Suy ra: 2AB < BE + BF
Vậy AB < (BE + BF) / 2 .