Cho (O) và điểm M nằm ngoài đường tròn (O). Từ M kẻ hai tiếp tuyến MA,MB với đường tròn (O)(A,B là các tiếp điểm). Qua M kẻ cát tuyến MCD với đường tròn (O) sao cho điểm C nằm giữa hai điểm M và D. a)Chứng minh tứ giác MAOB nội tiếp b)Gọi H là giao điểm của MO và AB. Chứng minh: MC.MD=MA^2. Từ đó suy ra MC.MD=MH.MO c)Lấy K là trung điểm của CD. Gọi E là giao điểm của BA và OK. Chứng minh EC là tiếp tuyến của (O)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Phải vì góc này tạo bởi tiếp tuyến MA và day cung AB
b: Xét ΔMOA vuông tại A có cosMOA=OA/OM=1/2
=>góc MOA=60 độ
sđ cung AB=2*60=120 độ
c: Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB tại H
=>MH*MO=MA^2
Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>MA/MD=MC/MA
=>MA^2=MD*MC=MH*MO

a: ΔOCD cân tại O có OK là đường trung tuyến
nên OK vuông góc CD
góc OKM=góc OAM=góc OBM=90 độ
=>O,K,M,A,B cùng thuộc đường tròn đường kính OM
b: Xét ΔMAC và ΔMDA có
góc MAC=góc MDA=1/2sđ cung AC
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>MA/MD=MC/MA
=>MA^2=MD*MC
=>MD*MC ko phụ thuộc vào cát tuyến MCD

Xét ΔMBC và ΔMDB có
góc MBC=góc MDB
góc BMC chung
=>ΔMBC đồng dạng với ΔMDB
=>MB/MD=MC/MB
=>MB^2=MD*MC

a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
b: Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>MA/MD=MC/MA
=>MA^2=MD*MC

a) Xét tứ giác OAMC có
\(\widehat{OAM}\) và \(\widehat{OCM}\) là hai góc đối
\(\widehat{OAM}+\widehat{OCM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: OAMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a: góc OAM+góc OCM=180 độ
=>OAMC nội tiếp
b: CE//BD
=>góc AKM=góc AEC=góc ACM
=>AKCM nội tiếp
=>A,K,C,M cùng nằm trên 1 đường tròn
=>góc OKM=90 độ
=>K là trung điểm của BD
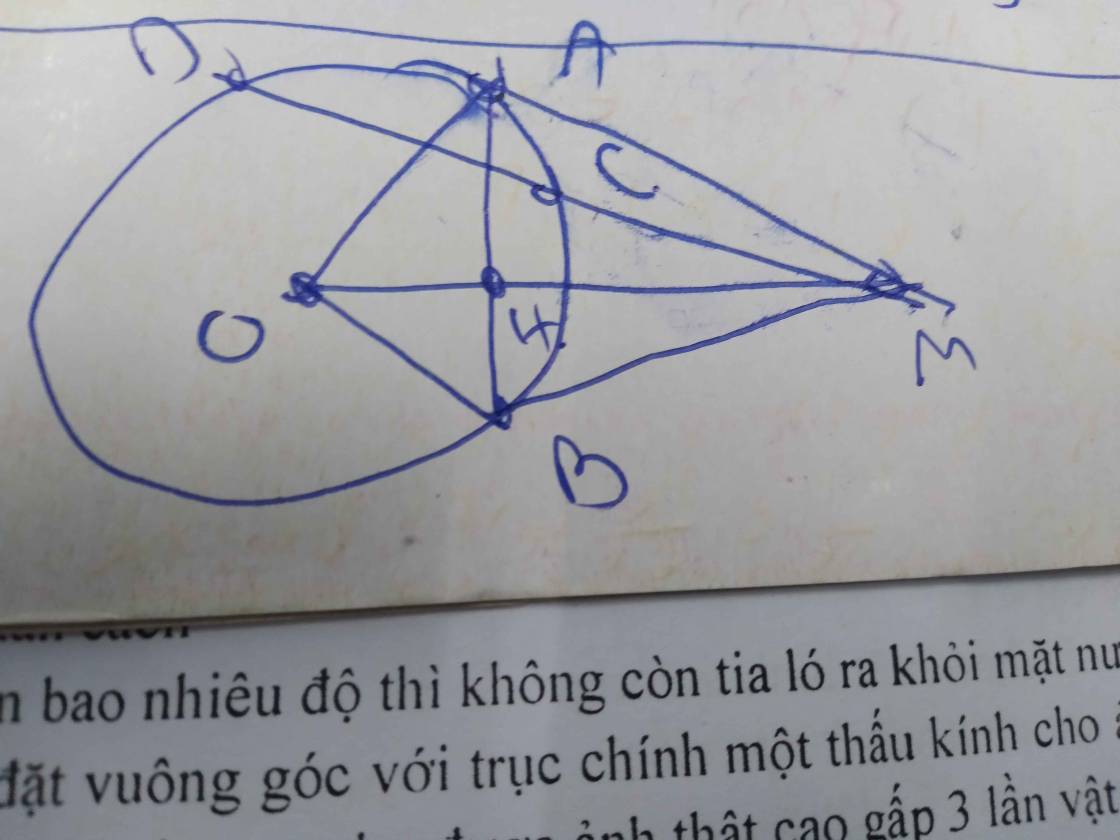



a) Xét tứ giác MAOB có
\(\widehat{OAM}\) và \(\widehat{OBM}\) là hai góc đối
\(\widehat{OAM}+\widehat{OBM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MAOB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét (O) có
\(\widehat{ADC}\) là góc nội tiếp chắn \(\stackrel\frown{AC}\)
\(\widehat{CAM}\) là góc tạo bởi dây cung CA và tiếp tuyến AM
Do đó: \(\widehat{ADC}=\widehat{CAM}\)(Hệ quả góc tạo bởi tia tiếp tuyến và dây cung)
hay \(\widehat{MDA}=\widehat{MAC}\)
Xét ΔMDA và ΔMAC có
\(\widehat{MDA}=\widehat{MAC}\)(cmt)
\(\widehat{AMD}\) là góc chung
Do đó: ΔMDA∼ΔMAC(g-g)
⇔\(\dfrac{MD}{MA}=\dfrac{MA}{MC}\)(Các cặp cạnh tương ứng tỉ lệ)
⇔\(MA^2=MC\cdot MD\)(đpcm)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔOAM vuông tại A có AH là đường cao ứng với cạnh huyền OM, ta được:
\(MA^2=MH\cdot MO\)(2)
Từ (1) và (2) suy ra \(MH\cdot MO=MC\cdot MD\)(đpcm)
c) để chứng minh EC là tiếp tuyến:
chứng minh tứ giác OECH nội tiếp thì ta sẽ có góc OHE=OCE=90o(đpcm)
=> cần chứng minh tứ giác OECH nội tiếp:
ta có: DOC=DHC (ccc CD)
xét MHC=MDO (tam giác MCH~MOD)= OCD (vì DO=OC)=OHD (cùng chắn OD) => HA là phân giác CHD
DOC=DHC => 1/2 DOC= 1/2 DHC =COE=CHE
mà COE với CHE cùng chắn cung CE trong tứ giác OHCE nên tứ giác đấy nội tiếp => xong :))))