Cách tính số trung bình cộng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
4 tháng 3 2020
Cách tính đúng là: \(\frac{a+b+c}{3}\)
Cách tính của bạn An là: \(\frac{\frac{a+b}{2}+c}{2}=\frac{a+b+2c}{4}\)
Ta có: \(\frac{a+b+c}{3}\)\(-\frac{a+b+2c}{4}\)
\(=\frac{4a+4b+4c-3a-3b-6c}{12}\)
\(=\frac{a+b-2c}{12}=\frac{\left(a-c\right)+\left(b-c\right)}{12}>0\)(vì a > b > c)
Vậy \(\frac{a+b+c}{3}\)\(>\frac{a+b+2c}{4}\)
=> đpcm...
PT
1
CM
28 tháng 12 2018
Để tính được các số trung bình cộng, phương sai, độ lệch chuẩn, trước hết ta cần lập bảng phân bố (tần số, tần suất, tần số ghép lớp hoặc tần suất ghép lớp).
* Đối với bảng phân bố tần số:
| Giá trị | x1 | x2 | x3 | … | xk | Cộng |
| Tần số | n1 | n2 | n3 | … | nk | N |
Số trung bình cộng:
Phương sai:
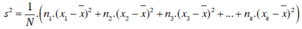
Độ lệch chuẩn:
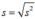
* Đối với bảng phân bố tần suất:
| Giá trị | x1 | x2 | x3 | … | xk | Cộng |
| Tần số | f1 | f2 | f3 | … | fk | 100% |
Số trung bình cộng:
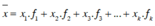
Phương sai:
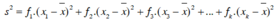
Độ lệch chuẩn:
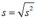
* Đối với bảng phân bố tần số ghép lớp:
| Lớp giá trị | [a1; a2) | [a2; a3) | [a3; a4) | … | [ak; ak+1] | Cộng |
| Giá trị đại diện | c1 | c2 | c3 | … | ck | |
| Tần số | n1 | n2 | n3 | … | nk | N |
Số trung bình cộng:
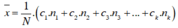
Phương sai:
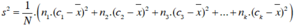
Độ lệch chuẩn:
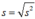
* Đối với bảng phân bố tần suất ghép lớp:
| Lớp giá trị | [a1; a2) | [a2; a3) | [a3; a4) | … | [ak; ak+1] | Cộng |
| Giá trị đại diện | c1 | c2 | c3 | … | ck | |
| Tần số | f1 | f2 | f3 | … | fk | 100% |
Số trung bình cộng:
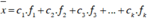
Phương sai:
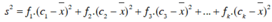
Độ lệch chuẩn:
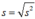
* Để tìm số trung vị (Me) ta sắp xếp dãy số liệu theo thứ tự nhỏ dần (hoặc lớn dần) rồi lấy số chính giữa (nếu số lượng số liệu lẻ) hoặc trung bình cộng của hai số ở giữa (nếu số lượng số liệu chẵn)
* Để tìm mốt của dãy số liệu, ta xem xét xem số nào có tần số lớn nhất thì số liệu đó là mốt của dãy.
22 tháng 1 2016
cách tính trên sai
chỉ cần lấy (a+b+c):3 là ok
tick cko mình nhé
TH
1
NH
3 tháng 11 2016
b1: tính số số hạng lấy số lớn nhất - số bé nhất : khoảng cách + 1
b2: tính tổng lấy (số lớn nhất cộng số bé nhất) x số số hạng rồi: 2
b3 lấy tổng chia cho số số hạng
ooooooooook
SG
1
PD
26 tháng 1 2021
2.
Quy tắc tìm số trung bình cộng
Số trung bình cộng của một dấu hiệu được tính từ bảng tần số theo cách sau:
- Nhân từng giá trị với tần số tương ứng
- Cộng tất cả các tích vừa tìm được
- Chia tổng đó cho các giá trị (tức tổng các tần số)
Ta có công thức: \(\overline{X}=\dfrac{x_1n_1+x_2n_2+x_3n_3...+x_kn_k}{N}\)
Trong đó:
- Ý nghĩa: Số trung bình cộng thường được dùng làm "đại diện" cho dấu hiệu, đặc biệt là khi muốn so sánh các dấu hiệu cùng loại.
PD
26 tháng 1 2021
1. So với bản thống kê ban đầu thì bảng tần số ngắn gọn, dễ hiểu hơn giúp người xem dễ điều tra hơn để nhận xét, quan sát về các giá trị
PT
3
\(\text{Trung bình cộng = Tổng các số chia số các số hạng.}\)