Cho tam giác ABC có trung tuyến AM (A thuộc BC) và BM < AM. Chứng minh: góc A nhọn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 6 2023
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
c: BM=CM=3cm
=>AM=4cm
5 tháng 4 2022
a. Xét tam giác AMB và tam giác AMC:
AB = AC
AM chung
BM = CM (trung tuyến AM hạ từ A đến BC)
=> tam giác AMB = tam giác AMC
=> góc BAM = góc CAM (2 góc tương ứng)=>AM là tia phân giác của góc BACb. đề bài bị thiếuc. ta có BM = CM(cma) => BM = CM = \(\dfrac{BC}{2}\)= \(\dfrac{6}{2}\)= 3(cm) Áp dụng định lí Pi-ta-go vào tam giác ABM: AB2 = BM2 + AM2=> AM2 = AB2 - BM2 AM2 = 52 - 32 = 25 - 9 = 16(cm)=> AM = 4 cm
2 tháng 3 2022
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM vừa là đường cao vừa là đường phân giác
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
b: Ta có: ΔAHK cân tại A
mà AM là đường phân giác
nên AM là đường trung trực của HK
10 tháng 5 2021
Giải
Xét tam giác AMB và tam giác AMC
AM chung
AB=AC(gt)
MB=MC(AM là trung tuyến của tam giác ABC)
Vậy tam giác AMB= tam giác AMC(c.c.c)
Suy ra :góc BAM = góc CAM
Suy ra AM là hân giác của gócA
Ý b
Vì tam giác AMB= tam giác AMC(cmt)
suy ra
góc AMB= góc AMC
có góc AMB+AMC=180 độ
mà góc AMB=góc AMC=90 độ
Suy ra AM vuông góc với BC
tam giác AMB vuông tại B
Ý c
Vì MB=MC=3cm
Áp dụng định lý PI-TA-GO và tam giác vuông ta có
AB^2=MB^2+MA^2
25=9+MA^2
MA^2=16
MA=4cm
KV
11 tháng 3 2023
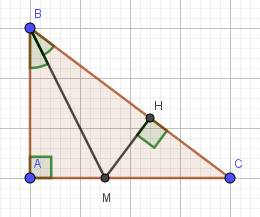
a) Xét hai tam giác vuông: \(\Delta AMB\) và \(\Delta HMB\) có:
BM là cạnh chung
\(\widehat{ABM}=\widehat{HBM}\) (do BM là phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta AMB=\Delta HMB\) (cạnh huyền-góc nhọn)
b) Do \(\Delta AMB=\Delta HMB\) (cmt)
\(\Rightarrow AM=HM\) (hai cạnh tương ứng)
c) \(\Delta MHC\) vuông tại H
\(\Rightarrow MC\) là cạnh huyền nên là cạnh lớn nhất
\(\Rightarrow HM< MC\)
Lại có HM = AM (cmt)
\(\Rightarrow AM< MC\)
TH
0