phát biểu định nghĩa hình thoi?vẽ hình minh hoạ vs nêu các tính chất cr hthoi?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 2 2017
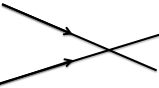
Hai đường thẳng phân biệt vuông góc với đường thẳng thứ ba thì chúng song song với nhau (hình a)
a⊥ c;b⊥c⇒ a//b
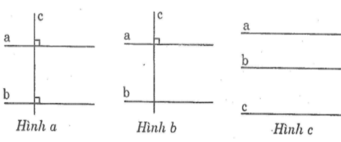
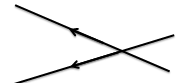
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia (hình b)
a//b; c⊥ a⇒ c ⊥ b
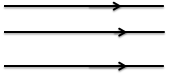
Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau (hình c)
a//c; b//c ⇒ a//b
LL
10 tháng 1 2022
TK:
“Trong một môi trường trong suốt và đồng tính, ánh sáng truyền đi theo đường thẳng. ” Ví dụ: Ánh sáng truyền trong không khí theo đường thẳng. Ánh sáng truyền trong môi trường nước theo đường thẳng.
Biểu diễn đường truyền của ánh sáng bằng đường thẳng có mũi tên gọi là tia sáng
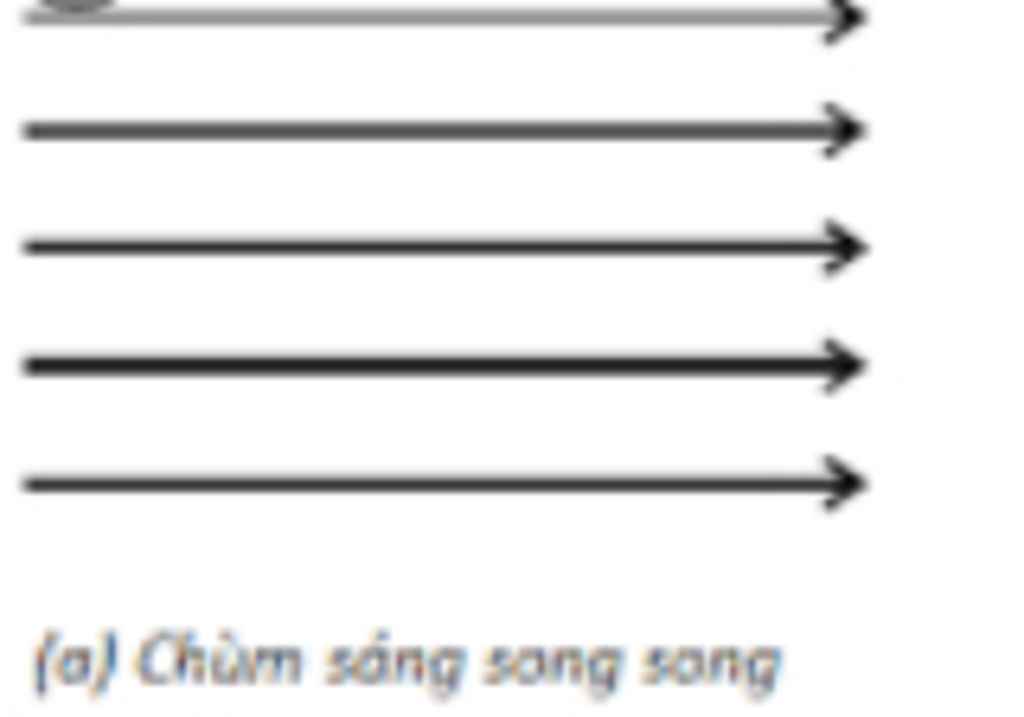
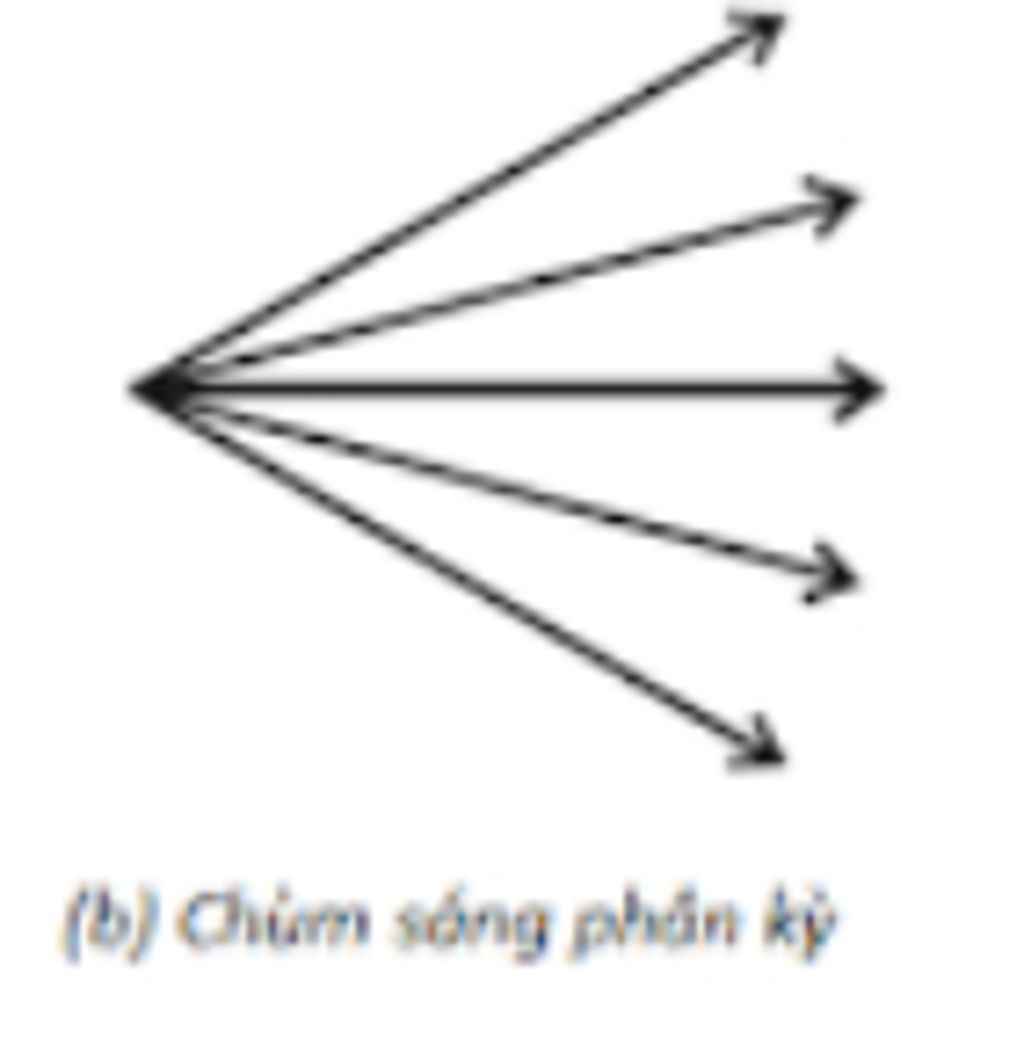
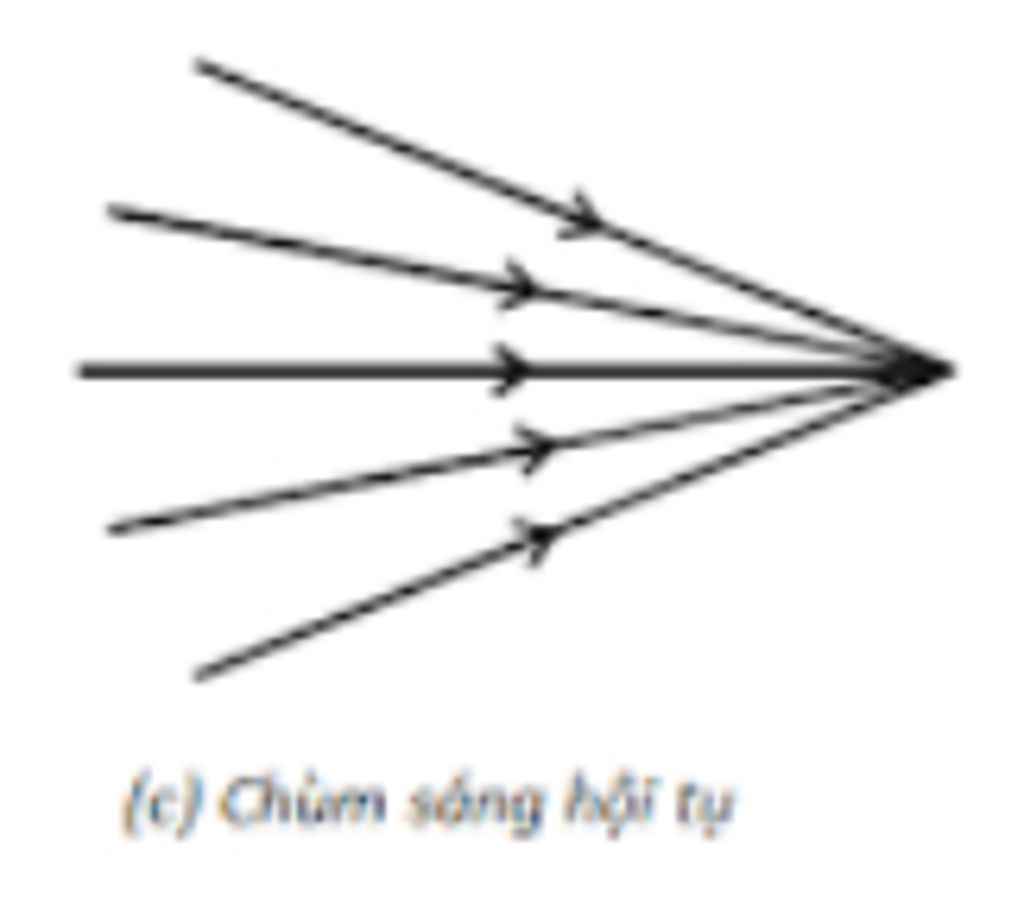
* Chùm sáng
- Chùm sáng gồm nhiều tia sáng hợp thành.
- Có ba loại chùm sáng:
+ Chùm sáng hội tụ: gồm các tia sáng giao nhau trên đường truyền của chúng.
+ Chùm sáng phân kì: gồm các tia sáng loe rộng ra trên đường truyền của chúng.
+ Chùm sáng song song: gồm các tia sáng không giao nhau trên đường truyền của chúng.
10 tháng 1 2022
TK:
- Trong môi trường trong suốt và đồng tính,ánh truyền đi theo đường thẳng.
- Đường truyền của ánh sáng được biểu diễn bằng một đường thẳng có hướng gọi là tia sáng
- Có 3 loại chùm sáng
+ Chùm sáng song song : Các tia sáng không giao nhau trên đường truyền đi của chúng
+ Chùm sáng phân kì : Các tia sáng loe rộng ra khi truyền đi
+ Chùm sáng hội tụ : Các tia sáng giao nhau trên đường truyền đi của chúng
0D
3
KS
8 tháng 9 2021
Tính chất ba đường trung tuyến của tam giác
Định lý: Ba đương trung tuyến của tam giác cùng đi qua điểm. điểm đó cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
Giao điểm của ba đường trung tuyến gọi là trọng tâm
GT : G là trọng tâm ∆ ABC
KL : AG/AD = BG/BE = CG/CF = 2/3
24 tháng 1 2017
1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông
C
2 tháng 2 2018
1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông
12 tháng 5 2021
Câu 1:
+ Tác dụng với kim loại: O2 oxi hóa được hầu hết các kim loại trừ Ag, Au, Pt
+ Tác dụng với Hiđro, Phản ứng có thể gây nổ mạnh nếu tỉ lệ phản ứng O2:H2 = 1:2
+ Tác dụng với một số phi kim khác:
+ Tác dụng với một số hợp chất:
Câu 2:
+ Phản ứng hóa hợp là PƯHH trong đó có một chất mới được tạo thành từ hai hay nhiều chất ban đầu.
+ Phản ứng phân hủy là PƯHH trong đó có 2 hay nhiều chất được tạo thành từ một chất ban đầu.
12 tháng 5 2021
Câu 2:
+ Phản ứng hóa hợp là PƯHH trong đó có một chất mới được tạo thành từ hai hay nhiều chất ban đầu.
+ Phản ứng phân hủy là PƯHH trong đó có 2 hay nhiều chất được tạo thành từ một chất ban đầu.
TT
1
H
16 tháng 12 2016
Định nghĩa :
_Tam giác cân là tam giác có hai cạnh bằng nhau.
Tính chất :
_Trong một tam giác cân hai góc ở đáy bằng nhau.
_Nếu một tam giác có hai góc bằng nhau thì là tam giác cân.
_Tam giác vuông cân là tam giác vuông có hai cạnh vuông góc bằng nhau.
Các cách chứng minh 1 tam giác là tam giác cân là :
_ 2 cạnh = nhau
_2 góc kề đáy = nhau
_ Tam giác có đường cao kẻ từ đỉnh là phân giác(trung tuyến, trung trực)
_Tam giác có một đường trung trực kẻ từ đỉnh
PT
1
CM
17 tháng 11 2018
- Hình bình hành là tứ giác có các cạnh đối song song.
- Hình chữ nhật là tứ giác có bốn góc vuông.
- Hình thoi là tứ giác có bốn cạnh bằng nhau.
- Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.
bốn cạnh bằng nhau
hai cạnh đối song song với nhau
2 đường chéo...và...vuông góc với nhau
k hỉu