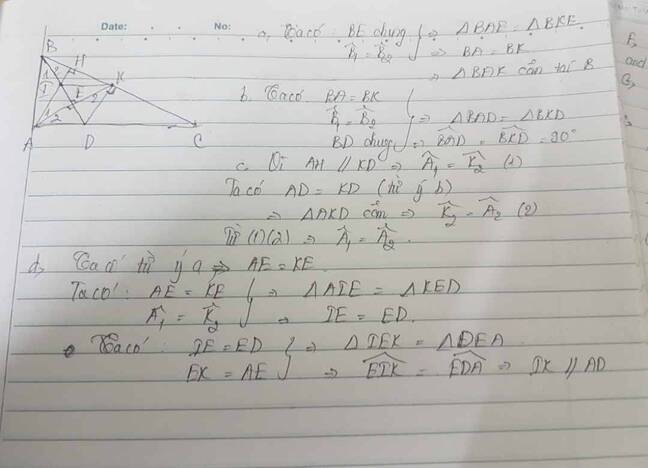Cho tam giác BCD nhọn có BC BD K = , là trung điểm CD . Từ K kẻ KE vuông góc BC tại E,KF vuông góc BD tại F . 1) Chứng minh rằng: = BCK BDK . 2) Chứng minh rằng: = BKE BKF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔBCK và ΔBDK có
BC=BD
CK=DK
BK chung
Do đó: ΔBCK=ΔBDK
b: Ta có; ΔBCK=ΔBDK
=>\(\widehat{CBK}=\widehat{DBK}\)
Xét ΔBEK vuông tại E và ΔBFK vuông tại F có
BK chung
\(\widehat{EBK}=\widehat{FBK}\)
Do đó: ΔBEK=ΔBFK
c: Ta có: ΔBEK=ΔBFK
=>EK=FK
Xét ΔKEM vuông tại E và ΔKFN vuông tại F có
KE=KF
\(\widehat{EKM}=\widehat{FKN}\)(hai góc đối đỉnh)
Do đó: ΔKEM=ΔKFN
=>ME=FN và KM=KN
Ta có: EK+KN=EN
KF+KM=FM
mà EK=KF
và KN=KM
nên EN=FM
d:
Ta có: ΔBEK=ΔBFK
=>BE=BF
Xét ΔBMN có \(\dfrac{BE}{EM}=\dfrac{BF}{FN}\)
nên EF//MN

a: Xét tứ giác AEKF có
\(\widehat{AEK}=\widehat{AFK}=\widehat{FAE}=90^0\)
Do đó: AEKF là hình chữ nhật

a) Áp dụng Pytago dễ dàng tính được AC=4
b) Xét hai tam giác vuông ABD và HBD có
BD cạnh chung
góc ABD = góc HBD (BD là phân giác góc B)
Nên hai tam giác trên bằng nhau (cạnh huyền - góc nhọn)
Suy ra AB = BH
AD = DH
Suy ra BD là trung trực của AH (định lý 2)
c) Ý bạn là E là giao điểm của AH và BD?
Hay E là giao điểm của DH và AB?

a. Xét Δ ABE và Δ KBE có:
^B1=^B2(BD là tia p/g)
^BEA=^KEB=90o
AE chung
=> ΔABE=ΔKBE(g.c.g)
=>AB=KB
=>ΔABK cân tại B
(xin lỗi mình ko biết phần b,c,d) ;-;
cho bạn cái hình nè :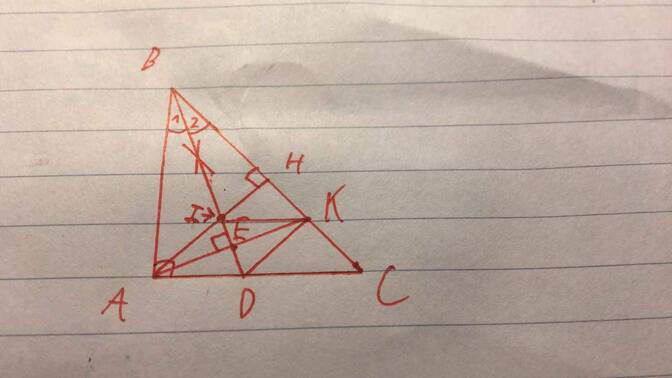

Nè bạn, tam giác ABC có vuông ko vậy
Nếu vuông thì mình mới làm được nhé.
Nhớ kết bạn với mình đó nha!

a: Xét tứ giác AEKF có
\(\widehat{AEK}=\widehat{AFK}=\widehat{FAE}=90^0\)
Do đó: AEKF là hình chữ nhật
b: Xét tứ giác AEFH có
AE//FH
AE=FH
Do đó: AEFH là hình bình hành