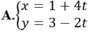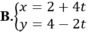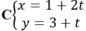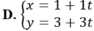Đoạn thẳng AB nối các điểm (-3, 11) và (5, 9). Tìm phương trình PQ, đường trung trực của AB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 8 2017
Gọi M trung điểm của AB nên M( 2; 1)
Ta có 
Gọi d là đường thẳng trung trực của AB
thì d qua M(2; 1) và nhận 
làm VTPT.
Phương trình đường thẳng d là:
1( x- 2) – 6.(y -1) =0
Hay x- 6y+ 4= 0.
Chọn D
11 tháng 1 2016
\(\overrightarrow{PQ}=(-4;-2)=2(2;1)\)
a) Đường thẳng qua A(3;2) song song với PQ nhận \(\overrightarrow{PQ}=(-4;-2)=2(2;1)\) làm VTCP nên có pt
\(\dfrac{x-3}{2}=\dfrac{y-2}{1}\Leftrightarrow x-2y+1=0\)
b) Đường thẳng trung trực của PQ qua trung điểm của PQ là M(2;-1) và nhận \(\overrightarrow{PQ}=(-4;-2)=2(2;1)\)làm VTPT nên có pt
\(2(x-2)+(y+1)=0\Leftrightarrow 2x+y-3=0\)
CM
30 tháng 3 2017
Gọi M( 1; 3) là trung điểm của AB.
Ta có 
Gọi d là đường thẳng trung trực của AB thì d qua M( 1;3) và nhận 
làm VTCP nên có phương trình tham số là:
Chọn A.
CM
20 tháng 7 2019
Chọn đáp án B
Gọi I là trung điểm AB và (P) là mặt phẳng trung trực của AB.
Ta có I là trung điểm AB nên I(-1;1;-2)
Lại có A B ⇀ = 4 ; - 8 ; - 6 và A B ⊥ P nên mặt phẳng (P) có một vectơ pháp tuyến là n ⇀ = 2 ; - 4 ; - 3 .
Phương trình mặt phẳng:
