Cho góc xAy và đường tròn (o) tiếp xúc với Ax và Ay tại B và C trên đoạn thẳng BC lấy điểm M ( M # B và C ) . Đường thẳng vuông góc với OM tại M cắt Ax,Ay lần lược tại D và E . Chứng minh các điểm A,D,O,E nằm trên một đường tròn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc CEM+góc CDM=180 độ
=>CEMD nội tiếp
b: góc EDM=góc ECM
góc FDM=góc FBM=góc ABM
=>góc EDF=góc ACM+góc ABM=60 độ

A B x C y D E F M
a/
D và E cùng nhìn MC dưới 1 góc vuông -> CDME là tứ giác nội tiếp
b/
CM tương tự ta cũng có tứ giác BDMF là tứ giác nội tiếp
\(\Rightarrow\widehat{MBF}=\widehat{MDF}\) (góc nt cùng chắn cung MF) (1)
Xét tứ giác nt CDME có
\(\widehat{MCE}=\widehat{MDE}\) (góc nt cùng chắn cung MF) (2)
Từ (1) và (2) \(\Rightarrow\widehat{MBF}+\widehat{MCE}=\widehat{MDF}+\widehat{MDE}=\widehat{EDF}\) (3)
Xét \(\Delta ABC\) có
AB=AC (Hai tiếp tuyến cùng xp từ 1 điểm)
=> \(\Delta ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}=\dfrac{180^o-\widehat{xAy}}{2}=\dfrac{180^o-60^o}{2}=60^o\)
Ta có
\(sđ\widehat{ABC}=\dfrac{1}{2}sđ\) cung BC => sđ cung BC = 2.sđ \(\widehat{ABC}=2.60^o=120^o\)
=> sđ cung BM + sđ cung CM = sđ cung BC \(=120^o\)
Ta có
\(sđ\widehat{MBF}=\dfrac{1}{2}sđ\) cung BM (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{MCE}=\dfrac{1}{2}sđ\) cung CM (góc giữa tiếp tuyến và dây cung)
\(\Rightarrow sđ\widehat{MBF}+sđ\widehat{MCE}=sđ\widehat{EDF}=\dfrac{sđcungBM+sđcungCM}{2}=\dfrac{sđcungBC}{2}=\dfrac{120^0}{2}=60^o\)
c/
Xét tg vuông MBF và tg vuông MCD có
\(sđ\widehat{MBF}=\dfrac{1}{2}sđcungBM\) (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{MCD}=\dfrac{1}{2}sđcungBM\) (góc nt)
\(\Rightarrow\widehat{MBF}=\widehat{MCD}\) => tg MBF đồng dạng với tg MCD
\(\Rightarrow\dfrac{MF}{MD}=\dfrac{MB}{MC}\)
CM tương tự ta cũng có tg vuông MCE đồng dạng với tg vuông MBD
\(\Rightarrow\dfrac{ME}{MD}=\dfrac{MC}{MB}\Rightarrow\dfrac{MD}{ME}=\dfrac{MB}{MC}\)
\(\Rightarrow\dfrac{MF}{MD}=\dfrac{MD}{ME}\Rightarrow MD^2=ME.MF\left(đpcm\right)\)

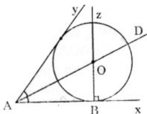
Đường tròn (O) tiếp xúc với hai tia Ax và Ay nên tâm O của (O) nằm trên tia phân giác của góc xAy

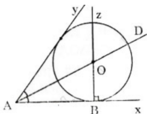
Đường tròn (O) tiếp xúc với hai tia Ax và Ay nên tâm O của (O) nằm trên tia phân giác của góc xAy. (Xem lại Bài 28 trang 116 SGK Toán 9 Tập 1) . Do đó ta có cách dựng:
- Dựng tia phân giác At của góc xAy.
- Dựng đường thẳng Bz qua B và vuông góc với tia Ax.
- Giao điểm O của At và Bz là tâm của đường tròn cần dựng.
- Dựng đường tròn tâm O, bán kính R = OB, ta được đường tròn cần dựng.


Cách dựng:
– Dựng tia phân giác At của góc xAy
– Dựng đường thẳng Bz qua B và vuông góc với tia Ax
– Giao điểm O của At và Bz là tâm của đường tròn cần dựng.
– Dựng đường tròn tâm O, bán kính R = OB, ta được đường tròn cần dựng.