S có 128 phần tử hỏi S có bao nhiêu tập hợp con
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 1 2018
Chọn A
Cách 1.
Giả sử 
Đặt 
Khi đó
C
1
,
C
2
, C là ba tập con không giao nhau của S và S =
C
1
∪
C
2
∪
C
Khi đó mỗi phần tử x ∈ S có 3 khả năng: Hoặc thuộc tập C 1 hoặc thuộc tập C 2 hoặc thuộc tập C.
Do đó 12 phần tử sẽ có 3 12 cách chọn.
Trong các cách chọn nói trên có 1 trường hợp C 1 = C 2 = ∅ , C = S
Các trường hợp còn lại thì lặp lại 2 lần (đổi vai trò C 1 và C 2 cho nhau).
Do đó số cách chia là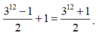 
Cách 2.
Đặt S = S 1 ∪ S 2
Nếu
S
1
có k phần tử 
Vậy số cách chọn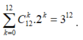 
Nhưng trường hợp 
giống nhau và không hoán vị nên có 
cách
8 tháng 8 2015
bài 1
6 tập hợp con
bài 2
{1};{2};{3};{1;2};{1;3};{2;3}
a){1;2};{1;3};{2;3}
b)có 0
c)có 0
d)6
21 tháng 9 2022
Bài 1 bạn kia trả lời sai nhé. Có 7 tập hợp con. Tập hợp con thứ 7 chính là tập hợp rỗng. Vì tập rỗng là tập hợp con của mọi tập hợp bạn nhé
13 tháng 9 2018
có 5 tập hợp con có 1 phần tử có nghĩ là tập hợp M có 5 phần tử.
Cho 5 phần tử đó là a,b,c,d,e thuộc tạp hợp M.
Tập hợp con của tập hợp M là:
C={a;b;c} A={a;b;d} F={a;c;e} D={b;c;d}
E={a;b;e} G={a;c;d} H={a;d;e} B={b;c;e}
L={c;d;e}
=>Tập hợp M có 9 tập hợp con có 3 phần tử.
18 tháng 9 2016
cho tập hợp a {0;2;4;6;8} viết tập hợp a có một phần tử
có bao nhiêu tập hợp con của a có 2 phần tử
có bao nhiêu tap hợp con của a có 4 phần tử
co bao nhieu tập hợp con của a có 3 phần tử
a) có 16
b) có 4
c) có 5
25 tháng 9 2019
tập hợp con của A có 1 phần tử là {0};{2};{4};{6};{8}
có 10 tập hợp con của A có 2 phần tử
có 2 tập hợp con của A có 4 phần tủ
tập hợp con có 3 phần tử là {0;2;4};{0;6;8};{2;4;6};{2;4;8};{2;6;8};{4;6;8}
có 1 tập hợp con có 5 phần tử
tập hợp A có 12 tập hợp con
mk ngu lắm, mk chỉ trả lời thôi
ko bt có đúng ko
XO
29 tháng 8 2021
Để x < 0
=> a - 20 < 0
=> a < 20 (1)
mà a \(\inℕ^∗\)(2)
Từ (1) và (2) => \(a\in\left\{1;2;3;...;19\right\}\)
=> Số phần tử của tập S là : (19 - 1) : 1 + 1 = 19 phần tử
s co 2^128 =............
ua ji ma nhieu the