Chứng minh không tồn tại x và y để: x2 + y2 = 1999
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^2+2y^2-2xy+x-2y+1=0\)
\(4x^2+8y^2-8xy+4x-8y+4=0\)
\(4x^2-4x\left(2y-1\right)+\left(2y-1\right)^2+8y^2-8y+4-\left(2y-1\right)^2=0\)
\(\left(2x-2y+1\right)^2+\left(4y^2-4y+1\right)+3=0\)
\(\left(2x-2y+1\right)^2+\left(2y-1\right)^2+3=0\) ( vô lí)
=> KL...........

Chọn C.
Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.
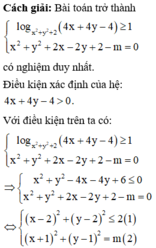


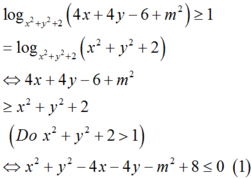
Ta có
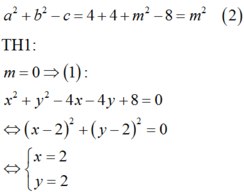
Cặp số x ; y = 2 ; 2 không thỏa mãn điều kiện .
![]()
Tập hợp các cặp số (x;y) thỏa mãn (1) là hình tròn C1(kể cả biên) tâm I1(2;2) bán kính R 1 = m .
Tập hợp các cặp số (x;y) thỏa mãn (2) là đường tròn C2 tâm I 2 - 1 ; 2 bán kính R 2 = 1 + 4 - 1 = 2 .
Để tồn tại duy nhất cặp số (x;y) thỏa mãn 2 điều kiện (1) và (2) Xảy ra 2 trường hợp sau:
TH1: C1; C2tiếp xúc ngoài
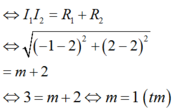
TH2: C1; C2 tiếp xúc trong và
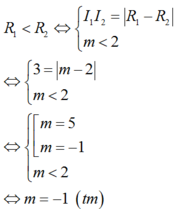
Vậy S = - 1 ; 1 .
Chọn D.

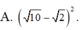
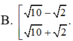
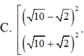


((x+y)/ 2)3=1999