Cho góc xOy nhọn. Lấy điểm A trên tia Ox; B trên tia Oy sao cho
OA=OB. Qua A kẻ đường thẳng vuông góc với tia Ox, cắt tia Oy tại M.
Qua B kẻ đường thẳng vuông góc với tia Oy, cắt tia Ox tại N. H là giao
điểm của AM và BN. I là trung điểm của MN. CMR:
a) OM=ON
b) Δ ANM= Δ BMN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

y x O M A B 1 2
Xét tam giác OMA và tam giác OMB ,có :
OM chung
góc O1 = góc O2 ( gt )
OA = OB ( gt )
=> tam giác OMA = tam giác OMB ( c-g-c )
=> MA = MB ( hai cạnh tương ứng )
=> tam giác AMB cân tại A
Vậy tam giác AMB cân

Góc AIB = 180 độ - 1/2 BAC - ABI
Góc AIC = 180 độ - 1/2 BAC - ACI
⇒ AIB + AIC = 180 độ - BAC - (ABI + ACI)
Giả sử B, I, C thẳng hàng
⇒BIC = 180 độ = AIB + AIC
→360 độ - BAC - (ABI + ACI) = 180 độ
ABI + ACI = 180 độ - BAC (LĐ)
Vậy điều giả sử là đúng
⇒B, I, C thẳng hàng

Bài 4:
a: Xét ΔABC vuông tại A và ΔABD vuông tại A có
BA chung
AC=AD
Do đó: ΔABC=ΔABD
b: Xét ΔMAC vuông tại A và ΔMAD vuông tại A có
MA chung
AC=AD
Do đó: ΔMAC=ΔMAD
Xét ΔMBD và ΔMBC có
MB chung
BD=BC
MD=MC
Do đó: ΔMBD=ΔMBC

Ta có hình vẽ:
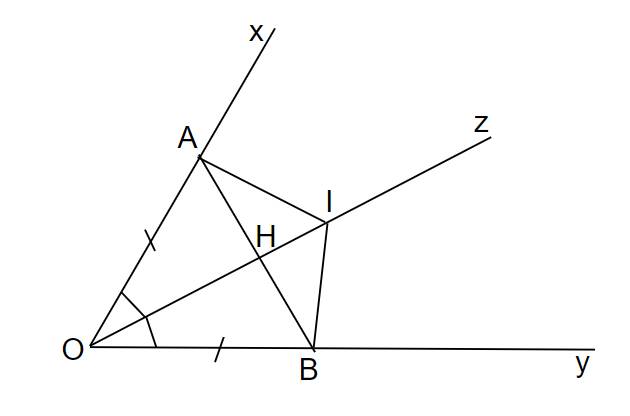
a) Vì Oz là phân giác của xOy nên xOz=yOz=xOy2���=���=���2
Xét Δ AOI và Δ BOI có:
OA = OB (gt)
AOI = BOI (cmt)
OI là cạnh chung
Do đó, Δ AOI = Δ BOI (c.g.c) (đpcm)
b) Xét Δ AOH và Δ BOH có:
OA = OB (gt)
AOH = BOH (câu a)
OH là cạnh chung
Do đó, Δ AOH = Δ BOH (c.g.c)
=> AHO = BHO (2 góc tương ứng)
Mà AHO + BHO = 180o (kề bù) nên AHO = BHO = 90o
=> AB⊥OI(đpcm))

a: Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
=>ΔOAC=ΔOBC
b: ΔOAC=ΔOBC
=>góc OBC=90 độ
=>CB vuông góc Oy
c: OA=OB
CA=CB
=>OC là trung trực của AB
a) Xét tam giác OAM và tam giác OBN có:
+ OA = OB (gt).
+ ^NOM chung.
+ ^OAM = ^OBN (= 90o).
=> Tam giác OAM = Tam giác OBN (c - g - c).
=> OM = ON (2 cạnh tương ứng).
b) Xét tam giác ANM vuông tại A và tam giác BMN vuông tại B:
+ MN chung.
+ AM = BN (Tam giác OAM = Tam giác OBN).
=> Tam giác ANM vuông tại A = Tam giác BMN vuông tại B (cạnh huyền - cạnh góc vuông).